როგორ შევადაროთ მონაცემთა ერთობლიობები
ყველა თქვენგანმა იცის როგორ უნდა შევადაროთ ორი ერთობლიობა, რომლებიდანაც თითოეული მხოლოდ ერთი მონაცემისაგან შედგება. ან როგორ შევადაროთ მონაცემთა ერთობლიობის ერთი წარმომადგენელი, სხვა მონაცემებს, როდესაც მონაცემთა ერთობლიობა მხოლოდ ორი მონაცემისაგან შედგება. ეს ორივე შემთხვევა დაიყვანება მხოლოდ ორი რიცხვის შედარებაზე. მაგრამ ვითარება გაცილებით რთულია, როდესაც ერთობლიობებში მონაცემთა რაოდენობა ორზე მეტია (და ხშირად გაცილებით მეტიც).
წარმოვიდგინოთ ასეთი ვითარება: თქვენ სწავლობთ ჯგუფში, რომელიც თქვენ გარდა კიდევ 4 წევრისაგან შედგება. მასწავლებელმა ჩაატარა 5 ქულიანი წერითი საკონტროლო. გასწორებული ფურცლების უკან დაბრუნების შემდეგ თქვენ შეიტყვეთ, რომ მიიღეთ 3 ქულა. როგორი იქნება თქვენი რეაქცია? გაგეხარდებათ თუ არა? როგორ უნდა შეაფასოთ თქვენი შედეგი? შეიძლება თქვენი რეაქცია იმით განისაზღვროს, რომ უბრალოდ გამოიანგარიშოთ თქვენ მიერ მიღებული ქულების პროცენტული რაოდენობა და იფიქროთ რომ ![]() არც ისე ცუდია. მაგრამ უფრო ბუნებრივი იქნება თუ შეეცდებით დამატებითი ინფორმაციის მოპოვებას. ასეთ შემთხვევებში მოსწავლეთა უმეტესობა ცდილობს გაიგოს სხვა მოსწავლეების შედეგები. სხვაგვარად რომ ვთქვათ, მოსწავლე ცდილობს შეადაროს თავისი შედეგი სხვებისას. თუ შედეგი ჯგუფის “მაღალ” შედეგებს შორისაა მაშინ სავარაუდოა, რომ მას გაუხარდება, ხოლო თუ “დაბალ” შედეგებს შორისაა – შეიძლება გული დაწყდეს.
არც ისე ცუდია. მაგრამ უფრო ბუნებრივი იქნება თუ შეეცდებით დამატებითი ინფორმაციის მოპოვებას. ასეთ შემთხვევებში მოსწავლეთა უმეტესობა ცდილობს გაიგოს სხვა მოსწავლეების შედეგები. სხვაგვარად რომ ვთქვათ, მოსწავლე ცდილობს შეადაროს თავისი შედეგი სხვებისას. თუ შედეგი ჯგუფის “მაღალ” შედეგებს შორისაა მაშინ სავარაუდოა, რომ მას გაუხარდება, ხოლო თუ “დაბალ” შედეგებს შორისაა – შეიძლება გული დაწყდეს.
შეიძლება ითქვას, რომ ცალკეული მონაცემის შედარება მონაცემთა მთლიან ერთობლიობასთან სტატისტიკის ერთ-ერთი ძირითადი ამოცანაა.
მაგალითისათვის განვიხილოთ ცხრილი, რომელშიც მოცემულია ჯგუფის შედეგების სამი შესაძლო ვარიანტი. მათ პირობითად ვუწოდოთ A, B , C და შევეცადოთ გავარკვიოთ რომელი მათგანი შეიძლება აღმოჩნდეს ჩვენთვის უფრო “სასიხარულო” (ან ნაკლებად “გულდასაწყვეტი”).
ცხრილი 1
| მოსწავლე | A | B | C |
| თქვენ | 3 | 3 | 3 |
| თეა | 3 | 4 | 2 |
| ზურა | 3 | 4 | 2 |
| გიორგი | 3 | 4 | 2 |
| ნინო | 3 | 5 | 1 |
A შემთხვევაში ყველა მოსწავლის შედეგი ერთნაირია. ამიტომ შეიძლება ითქვას, რომ თქვენი შედეგი მონაცემთა ერთობლიობის “შუაშია” და მიუხედავად იმისა, რომ 3 ქულა თავისთავად არც ისე მაღალი შედეგია, თქვენ შეიძლება უკმაყოფილო არ იყოთ რადგან სხვა მოსწავლეებსაც იგივე შედეგი აქვთ.
B შემთხვევაში, შედეგი ნამდვილად ვერ ჩაითვლება სასიხარულოდ. მართალია, იგი არ განსხვავდება იმ შედეგისაგან, რომელიც იყო A შემთხვევაში, მაგრამ ყველა დანარჩენს უფრო მაღალი შედეგი აქვს. შეიძლება ითქვას, რომ თქვენი შედეგი მონაცემთა ერთობლიობის “ცენტრის ქვემოთაა”.
C შემთხვევაში თქვენი შედეგი საუკეთესოა. ანალოგიური მოსაზრებით შეიძლება ითქვას, რომ აქ იგი მონაცემთა ერთობლიობის “ცენტრის ქვემოთაა”.
ჩვენი წარმოდგენა მონაცემთა ერთობლიობის ცენტრის შესახებ კიდევ უფრო რომ გავაღრმავოთ განვიხილოთ მაგალითი, რომელშიც ერთმანეთს ვადარებთ მონაცემთა ორი ერთობლიობის განლაგებას (და არა ცალკეულ მონაცემსა და მონაცემთა ერთობლიობას).
ქვემოთ მოყვანილ ცხრილის ფრაგმენტში მოცემულია ჭადრაკის პოზიციის დამხსოვრებასთან დაკავშირებული ექსპერიმენტის შედეგები. ექსპერიმენტის მონაწილეებს აჩვენებდნენ ჭადრაკის პოზიციას და შემდეგ სთხოვდნენ ამ პოზიციის აღდგენას ცარიელ დაფაზე. ყოველი ცდის შემდეგ იწერდნენ სწორად განლაგებული ფიგურების რაოდენობას. თითოეული ცდისპირისათვის ცდა განმეორდა სამჯერ და შედეგები შეჯამდა.
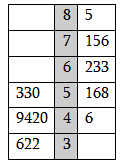
შენიშვნა:ამგვარი დიაგრამები ხშირად გამოიყენება მონაცემთა ორი ერთობლიობის შესადარებლად.
ცხრილის შუა სვეტი გვიჩვენებს დაგროვილი ქულების რაოდენობებს. პირველ სვეტში წარმოდგენილია იმ პირთა მონაცემები, რომლებიც ჭადრაკს არ თამაშობენ, ხოლო მესამე სვეტში იმ პირთა მონაცემები, რომლებიც სისტემატიურად თამაშობენ ჭადრაკს. დიაგრამის მიხედვით ალბათ ძნელი არ არის იმ დასკვნის გაკეთება, რომ ჭადრაკის მოთამაშეთა შესაბამის მონაცემთა ერთობლიობა უფრო “მაღლაა”.
სავარჯიშოები
1.მოცემულია მონაცემთა ორი ერთობლიობა 2, 3, 4, 9, 16 და 6, 9, 10, 15, 6. როგორ ფიქრობთ, რიცხვით ღერძზე რომელი ერთობლიობაა “განლაგებული” უფრო მარჯვნივ? შეეცადეთ დაასაბუთოთ.
2.განვიხილოთ მონაცემთა გამოსახვის ასეთი ხერხი. ყოველი რიცხვისათვის “ავიღოთ” ერთი და იგივე ზომის კვადრატი და რიცხვით ღერძზე დავადოთ ამ რიცხვის შესაბამის წერტილს. მაგალითად, 2, 3, 4, 9, 16 მონაცემების შემთხვევაში გვექნება ასეთი სურათი:
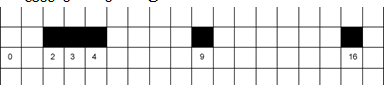
·როგორი სურათი იქნება 6, 9, 10, 15, 6 მონაცემებისათვის?
·როგორი სურათი იქნება -3, 0, 2, 1, 2, 3, 1, 3 მონაცემებისათვის?
3.გამოიყენეთ აღწერილი “გეომეტრიული” მოდელი მონაცემთა შემდეგი ერთობლიობების შესადარებლად:
1.2, 3, 4, 9, 16 და 6, 9, 10, 15, 6.
2.-9, 1, 3, 6, 1 და 5, -1, 1, 15, 4.
შენიშვნა:ამ დროს ადეკვატურია ისეთი მაგალითის განხილვა, რომელშიც გეომეტრიული ფიგურები ერთმანეთს ისე ფარავს, რომ მათი განლაგებების შედარება რთულია ამ დავალების მიზანია მოსწავლემ დამოუკიდებლად მოიფიქროს დიზაინის ისეთი ფორმა რომელიც შედარებაში დაეხმარება: კერძოდ, კვადრატები განალაგოს ღერძის სხვადასხვა მხარეს და გააფერადოს განსხვავებული ფერით. იხ. ნახაზი.
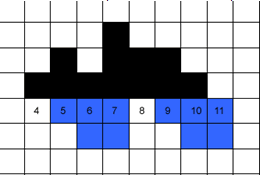
თუმცა, უნდა აღინიშნოს, რომ ჯერჯერობით, მონაცემთა შედარების ხერხი ინტუიციური წარმოდგენის ფარგლებს არ სცდება
4.მონაცემთა ერთობლიობას ეწოდება სიმეტრიული თუ ზემოაღწერილი ხერხით მიღებული გეომეტრიული ფიგურა ღერძულად სიმეტრიულია მონაცემთა დიაპაზონის შუაწერტილის მიმართ. ავიაკომპანიამ წლის პირველ კვარტალში შერჩეული 15 დღისათვის აღნუსხა ამ დღეებში გაუქმებული რეისების რაოდენობები. მიღებული მონაცემები ასეთია:
გაუქმებული რეისების რაოდენობა: 4, 9, 9, 12, 12, 13, 14, 14, 15, 15, 16, 16, 17, 17, 24. სიმეტრიულია თუ არა მონაცემთა ეს ერთობლიობა? რომელი მონაცემია მოდა? რისი ტოლია მისი სიხშირე?
5.აღწერილი გეომეტრიული მოდელის მიხედვით მოიფიქრეთ ფიზიკური მოდელი, რომელიც შეიძლება გამოვიყენოთ მონაცემთა ორი ერთობლიობის შესადარებლად.
მითითება: “მოატრიალეთ” სურათი ისე, რომ ღერძი “ვერტიკალურად” განლაგდეს. თავდაპირველად განიხილეთ ისეთი შემთხვევა, როდესაც მონაცემთა რაოდენობა ორივე ერთობლიობაში ტოლია.
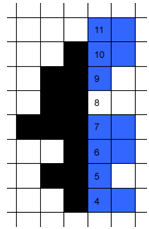
ამის შემდეგ, შეკითხვა – “რომელი ერთობლიობაა უფრო მარჯვნივ/მარცხნივ?”, შეიძლება დაისვას ასე – “რომელი გეომეტრიული ფიგურაა უფრო ზემოთ/ქვემოთ?”. წარმოვიდგინოთ, რომ თითოეული კვადრატი არის ფირფიტა, რომლის მასაა 1 გ., რის შემდეგაც შეკითხვა დავსვათ ასე: “რომელი სხეულია უფრო ზემოთ?”.
6.ვთქვათ მონაცემთა ორი ერთობლიობის განლაგების შედარებისას ვიყენებთ ამ ერთობლიობებში უმცირესი/უდიდესი მონაცემის ურთიერთგანლაგებას. კერძოდ, ვამბობთ, რომ A ერთობლიობა უფრო “მარცხნივაა” ვიდრე Bერთობლიობა თუ მისი უმცირესი მნიშვნელობა ნაკლებია. ანალოგიურად – უდიდესი მნიშვნელობისათვის. შედარეთ ეს ხერხი იმ ხერხს, რომელიც მოიფიქრეთ წინა სავარჯიშოში.
7.ვთქვათ მონაცემთა ორი ერთობლიობის შედარებისას ვიყენებთ მოდას (მონაცემს, რომელიც ყველაზე ხშირად გვხვდება). შედარეთ ეს ხერხი სხვა ხერხებს, რომლებიც აქამდე განვიხილეთ.
კომენტარი: ამ სავარჯიშოების მიზანია, მოსწავლე დამოუკიდებლად, ან მასწავლებლის დახმარებით მივიდეს მონაცემთა არითმეტიკული საშუალოს ცნებამდე და წარმოდგენა შეექმნას მის მნიშვნელობაზე მონაცემთა შედარებისას. გარდა ამისა, გარკვეული საფუძველი ჩაეყრება მომავალში სიხშირეთა განაწილებისა და ჰისტოგრამის ცნების გაგებას.
მონაცემთა ერთობლიობის მედიანა
მონაცემთა ერთობლიობის შესახებ გარკვეულ წარმოდგენას გვიქმნის მათი სიხშირეთა განაწილება. შეიძლება ითქვას, რომ სიხშირეთა განაწილება არის ასახვა, რომელიც თითოეულ მონაცემს შეუსაბამებს მის სიხშირეს – რიცხვს, რომელიც გვიჩვენებს, თუ რამდენჯერ შეგვხვდა ეს რიცხვი მონაცემთა ერთობლიობაში. სიხშირეთა განაწილებას ხშირად გამოსახავენ ცხრილის ან დიაგრამის საშუალებით.
მაგალითი: სასწავლო წლის განმავლობაში ჩატარებული საკონტროლოებში მოსწავლემ მიიღო ასეთი შეფასებები: 6, 7, 6, 8, 5, 7, 6, 9, 10, 6. ეს მონაცემები შეიძლება დაჯგუფდეს სიხშირეთა მიხედვით და გამოისახოს ასეთი ცხრილის საშუალებით:
| ქულა | სიხშირე |
| 5 | 1 |
| 6 | 4 |
| 7 | 2 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
იგივე განაწილება შეიძლება გამოისახოს ამგვარი დიაგრამის საშუალებითაც.
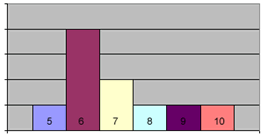
შეკითხვა: გაიხსენეთ წინა პარაგრაფში აღწერილი გეომეტრიული მოდელი, რომელიც გამოვიყენეთ მონაცემთა ორი ერთობლიობის შესადარებლად. რა კავშირი აქვს მას ამგვარ დიაგრამასთან?
როდესაც მოცემულია სიხშირეთა განაწილება (ცხრილის თუ დიაგრამის საშუალებით), იგი შეიძლება გამოვიყენოთ მონაცემთა ერთობლიობის საშუალოს მოსაძებნად.
შეკითხვა: როგორ ვიპოვოთ მონაცემთა ერთობლიობის არითმეტიკული საშუალო სიხშირეთა განაწილების საშუალებით? მოიფიქრეთ პროცედურა, რომლის გამოყენებითაც შეიძლება მონაცემთა არითმეტიკული საშუალოს მოძებნა სიხშირეთა განაწილების მიხედვით. შეადგინეთ შესაბამისი ალგებრული გამოსახულება.
როგორც ვნახეთ მონაცემთა ერთობლიობის არითმეტიკული საშუალო გარკვეულ წარმოდგენას გვიქმნის მონაცემთა ერთობლიობის განლაგებაზე. მეორე მნიშვნელოვანი მახასიათებელი, რომელიც გამოიყენება მონაცემთა ერთობლიობის განლაგების დასახასიათებლად არის მედიანა. იგი განისაზღვრება, როგორც რიცხვი, რომელიც მონაცემების დალაგების შემდეგ ზუსტად “შუაში” აღმოჩნდება. მაგალითად 9, 4, 16, 1, 5 მონაცემების შემთხვევაში, მედიანა არის 5. ხოლო 4, 5, 4, 3, 4, 5, 6 მონაცემების შემთხვევაში, მედიანა არის 4. რადგან ამ მონაცემების ზრდადობით დალაგების შემდეგ ვღებულობთ ასეთ მიმდევრობას: 3, 4, 4, 4, 5, 5, 6
ცხადია, რომ ამ მიმდევრობის შუა წევრია 4 (მის ორივე მხარეს წევრების რაოდენობები ტოლია).
შეკითხვა: რა შეიძლება იყოს მედიანა 9, 5, 2, 10, 3, 7 მონაცემების შემთხვევაში?
ალბათ მიხვდით, რომ როდესაც მონაცემთა რაოდენობა კენტია, მედიანა თვით ამ მონაცემთა ერთობლიობაში შემავალი რიცხვია. მაგრამ როდესაც მონაცემთა რაოდენობა ლუწია, მედიანა განისაზღვრება, როგორც იმ ორი რიცხვის საშუალო, რომლებიც მონაცემთა დალაგების შემდეგ მათ “შუაში” აღმოჩნდება. ე.ი. 9, 5, 2, 10, 3, 7 მონაცემების მედიანა იქნება 6. რადგან ზრდადობით დალაგების შემდეგ ვღებულობთ მიმდევრობას: 2, 3, 5, 7, 9, 10.
შეკითხვა: რა იქნება 9, 4, 16, 1, 5 მონაცემების არითმეტიკული საშუალო და მედიანა?
როგორც ვხედავთ მონაცემთა განლაგების (ცენტრალური ტენდენციის) ორი საზომის, არითმეტიკული საშუალოსა და მედიანას, მნიშვნელობები, ყოველთვის არ ემთხვევა ერთმანეთს.
ამოცანა: მოიფიქრეთ ისეთი 5 განსხვავებული მონაცემისაგან შემდგარი ერთობლიობის მაგალითი, რომელშიც მედიანა და საშუალო ერთმანეთის ტოლია.
სავარჯიშოები
1.უკანასკნელი წლების განმავლობაში ქალაქის საბჭო ღებულობდა საჩივრებს იმის შესახებ, რომ ავტომანქანების ნაკადის გაზრდის გამო სულ უფრო მეტად რთულდება მათავარი ქუჩის გადაკვეთა ბიბლიოთეკასთან ახლოს. საბჭომ გადაწყვიტა გამოიკვლიოს ავტომანქანების ნაკადი ამ ქუჩაზე. მათ აირჩიეს ადგილი იქ სადაც ბიბლიოთეკაში მიმავალი ადამიანები ყველაზე ხშირად კვეთდნენ ქუჩას და იწერდნენ ორიწუთიან ინტერვალში გამავალი ავტომანქანების რაოდენობას. ჩანაწერები გაკეთდა 10 ორწუთიანი ინტერვალისათვის, რამოდენიმე კვირის მანძილზე. მიღებული მონაცემები ასეთია:
ავტომანქანების რაოდენობა: 20, 27, 29, 28, 37, 23, 21, 28, 29, 28.
ამ მონაცემებისათვის იპოვეთ მედიანა და საშუალო.
2.რა გავლენას მოახდენს მედიანაზე და არითმეტიკულ საშუალოზე თუ მონაცემთა ერთობლიობაში, უდიდესი მნიშვნელობის მქონე მონაცემს კიდევ უფრო გავზრდით?
3.ერთმანეთს შედარეთ მონაცემთა განლაგების ორი მახასიათებელი: არითმეტიკული საშუალო და მედიანა:
·რა გავლენას მოახდენს მედიანაზე და არითმეტიკულ საშუალოზე თუ მონაცემთა ერთობლიობაში, უდიდესი მნიშვნელობის მქონე მონაცემს შევამცირებთ?
·ჩამოაყალიბეთ ზოგადად თუ რა გავლენას ახდენს მონაცემთა ერთობლიობის არითმეტიკულ საშუალოზე და მედიანაზე ამ ერთობლიობის ცალკეული მონაცემის ცვლილება (გაზრდა ან შემცირება)?
შეეცადეთ ჩამოაყალიბოთ თუ როდის რომელი საზომის გამოყენებაა უფრო ადეკვატური.
4.მესაკუთრეს სურს საწარმოს გაყიდვა. საჭიროა საწარმოს საწყისი ფასის დადგენა. ამისათვის გაყიდვების მენეჯერმა მოიწვია ექსპერტთა საბჭო. მოწვეული ექსპერტებიდან თითოეულმა უნდა დაასახელოს საწარმოს ღირებულება. გაყიდვების მენეჯერის მიზანია, ამ მონაცემების საფუძველზე დაასახელოს ადეკვატური ღირებულება. ექსპერტთა შორის, რომელიმეს მოსაზრებას უპირატესობა არ ენიჭება.
განიხილეთ შემთხვევები (წარმოდგენილი თანხის ერთი ერთეული 1,000,000 ლარის ტოლია):
a.მოწვეულია 2 ექსპერტი. მათ მიერ დასახელებული ღირებულებებია: 20 და 25.
b.მოწვეულია 3 ექსპერტი. მათ მიერ დასახელებული ღირებულებებია 21, 18, 26.
c.მოწვეულია 3 ექსპერტი. მათ მიერ დასახელებული ღირებულებებია 20, 15, 55.
შეეცადეთ განაზოგადოთ და ჩამოაყალიბოთ წესი, რომლითაც შეიძლება იხელმძღვანელოს გაყიდვების მენეჯერმა, მესაკუთრისათვის საწყისი ღირებულების შეთავაზებისას (3 ექსპერტის შემთხვევაში). გაითვალისწინეთ, რომ გაყიდვების მენეჯერმა მესაკუთრეს უნდა დაუსაბუთოს მის მიერ გამოყენებული წესის ეფექტიანობა.
ვთქვათ მოწვეულ ექსპერტებს შორის ერთ-ერთის მოსაზრებას ენიჭება გარკვეული უპირატესობა სხვა ექსპერტების მოსაზრებებთან შედარებით. როგორ შეიცვლებოდა ადეკვატური ღირებულების განსაზღვრის ხერხი?
კომენტარი
გაკვეთილის მიზანია მოსწავლეს ჩამოუყალიბდეს გარკვეული წარმოდგენები შესაფერისი შემაჯამებელი რიცხვითი მახასიათებლის შერჩევის შესახებ. შეძლოს თავისი არჩევანის დასაბუთება და მისი გამოყენება მონაცემთა ერთობლიობის დასახასიათებლად ან/და მონაცემთა ორი ერთობლიობის შესადარებლად.
საწყისი ცოდნა და უნარები: მოსწავლეს შეუძლია მონაცემთა დალაგება, დაჯგუფება და წარმოდგენა (ცხრილის სახით). იცის რას ეწოდება რიცხვის აბსოლუტური მნიშვნელობა და რიცხვითი მონაცემების ცენტრალური ტენდენციის საზომი –არითმეტიკული საშუალო.
განსაკუთრებით მნიშვნელოვანია 6-ე დავალება, რომლის შესრულებას ერთი გაკვეთილი არ ეყოფა. იგი უნდა დაიყოს საფეხურებად. რა თქმა უნდა, იშვიათ შემთხვევებში ამოცანა შეიძლება განზოგადდეს, მაგრამ VII კლასის მოსწავლის კომპეტენცია არასაკმარისია იმისათვის, რომ ამოცანა გასცდეს სამი მონაცემის (სამი ექსპერტის შემთხვევა). გარდა ამისა, ამ საფეხურზე ამგვარი განზოგადების აუცილებლობა არ არსებობს, რადგან ამოცანა გაცილებით ეფექტიანად ამოიხსნება მაღალ კლასებში, როდესაც მოსწავლეს ექნება მათემატიკური ინდუქციის გამოყენების უნარი და ეცოდინება წილად-წრფივი, თუ კვადრატული ფუნქციის მაქსიმუმის მოძებნა.
საჭიროების შემთხვევაში მონაცემთა რაოდენობა შეიძლება გაიზარდოს. მთავარია, რომ მოსწავლემ გაიგოს, რომ გაყიდვების მენეჯერის მიზანია ისეთი რიცხვის შერჩევა, რომელიც ყველაზე მეტად იქნება შეთანხმებული ექსპერტების მიერ დასახელებულ თანხებთან. ამისათვის შეიძლება დაისვას ასეთი სახის შეკითხვები:
·ექსპერტების მიერ მოწოდებული მონაცემების გათვალისწინებით, რომელი ღირებულება უფრო ადეკვატურია 21 თუ 30 (დასაწყისისათვის განიხილება a შემთხვევა, ხოლო შემდეგ ანალოგიური შეკითხვები დაისმება b და c შემთხვევებისათვისაც)?
მიზანი:მოსწავლემ დაადგინოს თუ რა შეიძლება იყოს “ადეკვატურობის საზომი”. კერძოდ, ადეკვატურობის საზომი შეიძლება იყოს ის თუ რამდენადაა “დაშორებული” ესა თუ ის ღირებულება ექსპერტის მიერ დასახელებული თანხისაგან. ე.ი. 21-ის შემთხვევაში გვექნება: 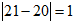 და
და 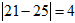 . ხოლო 30-ის შემთხვევაში გვექნება:
. ხოლო 30-ის შემთხვევაში გვექნება: 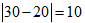 და
და 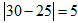 . ამ შემთხვევაში ნათლად ჩანს, რომ რიცხვი 21 უფრო “ახლოსაა” ექსპერტების მიერ დასახელებულ თანხებთან ვიდრე 30. შეიძლება შეირჩეს ისეთი რიცხვები (თუნდაც ორი ექსპერტის შემთხვევაში), როდესაც ეს ყოველივე ამდენად ცხადი არ არის და საჭიროა გარკვეული გამოთვლებს ჩატარება. როგორც პრაქტიკა გვიჩვენებს უმეტეს შემთხვევებში მოსწავლე ხვდება რომ მან მიღებული რიცხვები უნდა შეკრიბოს. ე.ი. 21-ის შემთხვევაში გვექნება:
. ამ შემთხვევაში ნათლად ჩანს, რომ რიცხვი 21 უფრო “ახლოსაა” ექსპერტების მიერ დასახელებულ თანხებთან ვიდრე 30. შეიძლება შეირჩეს ისეთი რიცხვები (თუნდაც ორი ექსპერტის შემთხვევაში), როდესაც ეს ყოველივე ამდენად ცხადი არ არის და საჭიროა გარკვეული გამოთვლებს ჩატარება. როგორც პრაქტიკა გვიჩვენებს უმეტეს შემთხვევებში მოსწავლე ხვდება რომ მან მიღებული რიცხვები უნდა შეკრიბოს. ე.ი. 21-ის შემთხვევაში გვექნება: 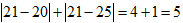 , ხოლო 30-ის შემთხვევაში გვექნება:
, ხოლო 30-ის შემთხვევაში გვექნება: 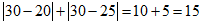 ; 5 ნაკლებია 15, ამიტომ 21 უფრო ადეკვატურია (უფრო მეტად ითვალისწინებს ექსპერტების მოსაზრებებს).
; 5 ნაკლებია 15, ამიტომ 21 უფრო ადეკვატურია (უფრო მეტად ითვალისწინებს ექსპერტების მოსაზრებებს).
დასკვნა: უნდა შეირჩეს ისეთი რიცხვი, რომლისთვისაც ექსპერტების მიერ დასახელებული რიცხვებიდან “დაშორებების” ჯამი უმცირესია. ეს უკვე მოდელის ზოგადი ფორმულირებაა, რომელიც რა თქმა უნდა საჭიროებს შემდგომ დახვეწას. ორი რიცხვის შემთხვევაში მოსწავლე ამჩნევს ამ რიცხვებს შორის მოთავსებული ნებისმიერი რიცხვისათვის ეს ჯამი ყოველთვის ერთი და იგივეა. შემდეგ ეტაპზე იგი იყენებს მანძილის თვისებებს და მკაცრად ასაბუთებს, რომ სწორედ ეს რიცხვია უმცირესი.
- ანალოგიური შეკითხვა მეორდება ბ და ც შემთხვევებისათვის. როგორც წესი, 3 მონაცემის კერძო შემთხვევებისათვის, მოსწავლეთა უმეტესობა ამჩნევს (ზოგჯერ მასწავლებლის დახმარებით), რომ საძიებელი რიცხვი არის ის რიცხვი, რომელიც დასახელებული რიცხვების “შუაშია”. ამის განზოგადება და დამტკიცება (3 მონაცემის შემთხვევაში), მანძილის თვისებების გამოყენებით, კვლავ დაძლევადი ამოცანაა. ამ ეტაპზე შესაძლებელია მედიანის ცნების შემოტანა.
- აუცილებელია მოსწავლის ყურადღება გავამახვილოთ იმ ფაქტზე, რომ ეს მოდელი ნაკლებად ითვალისწინებს იმ ექსპერტის აზრს რომლის მიერ დასახელებული თანხა მკვეთრად განსხვავდება სხვა ექსპერტების მიერ დასახელებული თანხებისაგან. ამ მიზნით შეიძლება გამოვიყენოთ ელექტრონული ცხრილი.
მიზანი:მოსწავლემ შეამჩნიოს მოდელის თვისებები. შეაფასოს მისი გამოყენების ადეკვატურობა ამა თუ იმ შემთხვევაში. როგორც წესი წარმოიშობა ამ ტიპის მოსაზრებები: “თუ რომელიმე ექსპერტის მოსაზრება მკვეთრად განსხვავდება სხვა ექსპერტების მოსაზრებებისაგან, ე.ი. საქმე რაღაცაშია . . . იქნებ გავზარდოთ ექსპერტების რაოდენობა (კიდევ ვინმეს ვკითხოთ . . .)”, ან “იქნებ სხვა მოდელი გამოვიყენოთ”. ამ უკანასკნელ შემთხვევაში ეს შეიძლება დავუკავშიროთ არითმეტიკული საშუალოს ცნებას. როგორც წესი, თუ ეს მახასიათებელი მათთვის უკვე ცნობილი არ არის, მოსწავლე თავისით ვერ აღმოაჩენს მას. ტექნოლოგიების გამოყენებით ვახდენთ იმის დემონსტრირებას, რომ მკვეთრად განსხვავებული მოსაზრება უფრო მეტ გავლენას ახდენს არითმეტიკულ საშუალოზე.
- შეკითვა: თუ მედიანა ისეთი რიცხვია, რომლის ჯამური გადახრა მონაცემებისაგან უმცირესია, რა სიდიდე ხდება უმცირესი საშუალო მნიშვნელობის შემთხვევაში?
ამ შეკითხვაზე მოსწავლეთა უმეტესობა დამოუკიდებლად ვერ პასუხობს. თუმცა ორი მონაცემის შემთხვევაში შესაძლებელია დავეყრდნოთ მათ ცოდნას ალგებრიდან და დამოუკიდებლად აღმოაჩინონ რომ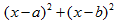 გამოსახულების მნიშვნელობა უმცირესია, მაშინ როდესაც
გამოსახულების მნიშვნელობა უმცირესია, მაშინ როდესაც 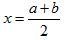 . იმ შემთხვევაში, როდესაც ამ სახის ალგებრული ამოცანები, გამოსახულების უმცირესი/უდიდესი მნიშვნელობის მოძებნაზე წინ უსწრებს ამ საკითხს, ბევრი მოსწავლე დამოუკიდებლად მიდის საჭირო დასკვნამდე.
. იმ შემთხვევაში, როდესაც ამ სახის ალგებრული ამოცანები, გამოსახულების უმცირესი/უდიდესი მნიშვნელობის მოძებნაზე წინ უსწრებს ამ საკითხს, ბევრი მოსწავლე დამოუკიდებლად მიდის საჭირო დასკვნამდე.
გვაქვს ორი მოდელი, რომლებიც შეიძლება ასე ჩამოყალიბდეს:
მედიანა – ისეთი სიდიდე x , რომლისათვისაც 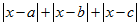 გამოსახულება ღებულობს უმცირეს მნიშვნელობას;
გამოსახულება ღებულობს უმცირეს მნიშვნელობას;
არითმეტიკული საშუალო – ისეთი სიდიდე x , რომლისათვისაც 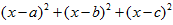 გამოსახულება ღებულობს უმცირეს მნიშვნელობას.
გამოსახულება ღებულობს უმცირეს მნიშვნელობას.
მონაცემთა ცვლილებით ამ ორი მოდელის შედარებისას, მოსწავლეებს დიდ დახმარებას გაუწევს ტექნოლოგიების გამოყენება (მაგალითად,ელექტრონული ცხრილი).


