საცხოვრებელი სახლის კიბის დაპროექტება

კიბის დაპროექტების აქტივობა მე-10 კლასელებისთვის აქტუალურია, რადგან ის მათემატიკურ ცოდნას, კონკრეტულად ტრიგონომეტრიას აკავშირებს ისეთ რეალურ საგნებთან, როგორიცაა, შენობების დიზაინი, რაც ზრდის სწავლის მოტივაციას. ამასთან, მას აქვს ინტერდისციპლინარული ხასიათი და მოიცავს საინჟინრო, დიზაინის, ერგონომიკისა და უსაფრთხოების ასპექტებს, რაც ჰოლისტური ხედვის ჩამოყალიბებას უწყობს ხელს. აქტივობა ავითარებს პრობლემის გადაჭრის, მათემატიკური მოდელირების, სივრცითი აზროვნების, კვლევითი, ჯგუფური მუშაობისა და კომუნიკაციის უნარებს, კრეატიულობასა და ინოვაციას დიზაინის ოპტიმიზაციის პროცესში.

წარმოგიდგენთ აქტივობებს, რომელთა საშუალებითაც მე-10 კლასელებმა შეძლეს მართკუთხა სამკუთხედში ტრიგონომეტრიული თანაფარდობების გამოყენება კიბის კონსტრუქციის პრინციპების გასაგებად.

მიმართულება: გეომეტრია და გაზომვა

თემატური ბლოკები:

• გეომეტრიული მოდელები, მათი გამოყენება რეალურ ცხოვრებაში (არქიტექტურა, დიზაინი და ა.შ.)
• ტექნოლოგიების გამოყენება გეომეტრიასა და ყოველდღიური პრობლემების გადაჭრაში

თემა: გეომეტრია და ტრიგონომეტრია

საკითხები:

• გეომეტრიული ობიექტები, გეომეტრიული ობიექტების აღწერა, კლასიფიკაცია; რეალურ ცხოვრებაში გეომეტრიული ფორმების ამოცნობა;
• ფიგურათა ტოლობა და მსგავსება;
• მართკუთხა სამკუთხედი და ტრიგონომეტრია; ტრიგონომეტრიული თანაფარდობები მართკუთხა სამკუთხედში და მათი გამოყენება რეალური პრობლემების გადასაჭრელად;

სამიზნე ცნებები:

 მათემატიკური მოდელი

მსგავსი სამკუთხედები, პროპორციული მონაკვეთები.

ტრიგონომეტრიული ფუნქციები

კანონზომიერება

ფიგურის ელემენტებს შორის კავშირების დადგენა;

გამოთვლები

ლოგიკა-ლოგიკური მსჯელობა; დასაბუთება მათემატიკურ თვისებებზე დაყრდნობით

სტანდარტის მიხედვით მისაღწევი შედეგები:

მათ.საშ.4. რეალურ ცხოვრებაში გეომეტრიული ფორმების ამოცნობა, აღწერა, კლასიფიკაცია; გეომეტრიული ობიექტების განსაზღვრებათა და თვისებათა სწორად ჩამოყალიბება; გეომეტრიული ობიექტის ზომის გამოთვლა;

აქტივობა1. კიბის გაზომვა

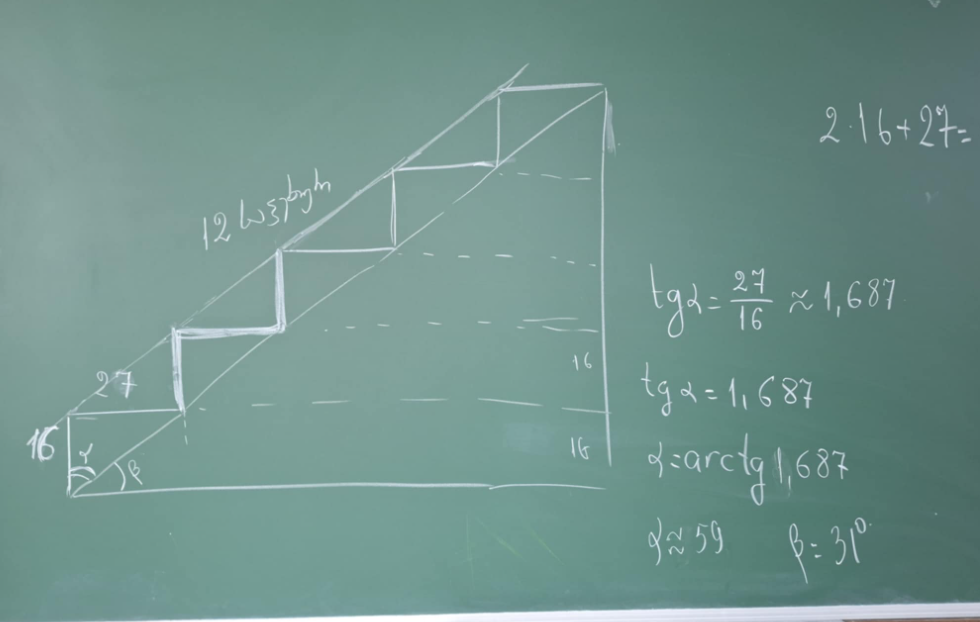
კომპლექსური დავალების დამოუკიდებლად შესრულებამდე მოსამზადებელ ეტაპზე, კლასში განვახორციელეთ პირველი აქტივობა: სკოლის მეორე სართულზე ასასვლელი კიბის ზომების დადგენა. მოსწავლეებმა მარტივი ხელსაწყოების გამოყენებით გაზომეს ერთი საფეხურის სიმაღლე და სიღრმე, შეასრულეს კიბის ესკიზური ნახაზი და გეომეტრიული ობიექტების თვისებებისა და ტრიგონომეტრიული თანაფარდობების გამოყენებით მართკუთხა სამკუთხედში განსაზღვრეს კიბის დახრის კუთხე. 

მოსწავლეებმა ერთმანეთს გაუზიარეს მიღებული შედეგები და იმსჯელეს, რამდენად კომფორტული და უსაფრთხოა გაზომილი კიბე ბლონდელის წესისა და დახრის რეკომენდებული კუთხის გათვალისწინებით. ამ პირველადმა პრაქტიკულმა გამოცდილებამ საფუძველი ჩაუყარა შემდგომ თეორიულ კვლევასა და დაპროექტების პროცესს.

აქტივობა 2. კომპლექსური დავალება

ამის შემდეგ შევთავაზე ალტერნატიული დიზაინის შექმნა, კომპლექსური დავალების სახით

• დავყავი მოსწავლეები ჯგუფებად, შევთავაზე თითოეულ ჯგუფს აირჩიოს კიბის საერთო სიმაღლის ერთ-ერთი ვარიანტი (1.5 მ ან 2.0 მ).
• მოსწავლეებს შესთავაზე შექმნან კიბის მინიმუმ ორი განსხვავებული დიზაინი შემდეგი ცვლადების (h, H, d…) შეცვლით, თითოეული არჩეული დიზაინისთვის მოსწავლეებმა ხელახლა გამოთვალონ შემდეგი პარამეტრები ტრიგონომეტრიული თანაფარდობების გამოყენებით, და შეაფასონ რა დადებითი და უარყოფითი მხარეები აქვს თითოეულ დიზაინს (მაგალითად, მეტი საფეხური ნიშნავს ნაკლებ დახრილობას, მაგრამ მეტ ადგილს იკავებს ჰორიზონტალურად…) მოსწავლეებმა უნდა დაასაბუთონ თავიანთი არჩევანი, ახსნან, რატომ მიიჩნევენ კონკრეტულ დიზაინს უფრო უსაფრთხოდ და კომფორტულად. შევთავაზე მათ კომპლექსური დავალების პირობა.

კომპლექსური დავალება სათაური: საცხოვრებელი სახლის კიბის დაპროექტება სასწავლო თემა: ტრიგონომეტრიული თანაფარდობები მართკუთხა სამკუთხედში მიზანი: ·         მოსწავლეებმა შეძლონ მართკუთხა სამკუთხედში ტრიგონომეტრიული თანაფარდობების (სინუსი, კოსინუსი, ტანგენსი) გამოყენებას რეალური საინჟინრო ამოცანის გადასაჭრელად. მოსწავლეებმა განავითარონ პრობლემის გადაჭრის, მათემატიკური მოდელირების, სივრცითი აზროვნებისა და პრეზენტაციის უნარები. დავალების პირობა: წარმოიდგინეთ, რომ თქვენ ხართ არქიტექტორი ან დიზაინერი და გევალებათ დააპროექტოთ კიბე საცხოვრებელი სახლისთვის. კიბე უნდა აკავშირებდეს მიწის დონეს სახლის შესასვლელ კართან, რომელიც მიწის ზედაპირიდან 1.5 მეტრის ან 2 მეტრის სიმაღლეზე მდებარეობს (აირჩიეთ ერთ-ერთი ვარიანტი). თქვენი ამოცანაა, გამოიყენოთ მართკუთხა სამკუთხედში ტრიგონომეტრიული თანაფარდობები, რათა შექმნათ კიბის ოპტიმალური, უსაფრთხო და კომფორტული დიზაინი. შესასრულებელი ეტაპები: საწყისი მონაცემების შერჩევა: აირჩიეთ და დააფიქსირეთ კიბის საერთო სიმაღლე (H): 1.5 მ ან 2.0 მ. კვლევა და საფეხურების პარამეტრების განსაზღვრა: მოიძიეთ ინფორმაცია კიბის საფეხურების რეკომენდებული ზომების შესახებ (სიმაღლე და სიღრმე). შეარჩიეთ ერთი საფეხურის ოპტიმალური სიმაღლე (h) და სიღრმე (d). გაითვალისწინეთ, რომ კომფორტული საფეხურის სიმაღლე, როგორც წესი, 15 სმ-დან 18 სმ-მდეა, ხოლო სიღრმე – 25 სმ-დან 30 სმ-მდე.  (სურვილისამებრ) გაითვალისწინეთ ბლონდელის წესი კიბის კომფორტულობისთვის: 2h+d≈60−65 სმ. „მე-17 საუკუნის ფრანგმა არქიტექტორმა, ფრანსუა ბლონდელმა, კარგად იცოდა კიბის დიზაინში კომფორტის მნიშვნელობა. მან შეიმუშავა ფორმულა, რომელიც ცნობილია როგორც ბლონდელის ფორმულა: 2 საფეხური (სიმაღლე) + 1 საფეხური (სიღრმე) = 25 ინჩი (63-65 სმ) . ეს ფორმულა არქიტექტურის ოქროს წესია, რომელიც არქიტექტორებს ეხმარება კიბეების გამოთვლაში, რომლებზეც სიარული სასიამოვნოა“.   გამოთვლები ტრიგონომეტრიის გამოყენებით: საფეხურების რაოდენობა (N): გამოთვალეთ საფეხურების საერთო რაოდენობა (N=H/h). იმსჯელეთ, როგორ უნდა დამრგვალდეს მიღებული მნიშვნელობა და როგორ აისახება ეს საფეხურების ზუსტ სიმაღლეზე (შეეცადეთ, ყველა საფეხურს ერთნაირი სიმაღლე ჰქონდეს). კიბის საერთო ჰორიზონტალური სიგრძე (L): გამოთვალეთ კიბის მიერ დაკავებული საერთო ჰორიზონტალური მანძილი (L=N×d). კიბის დახრის კუთხე (α): განიხილეთ კიბე, როგორც მართკუთხა სამკუთხედის ჰიპოტენუზა, სადაც ვერტიკალური კათეტია H (კიბის საერთო სიმაღლე) და ჰორიზონტალური კათეტია L (კიბის საერთო ჰორიზონტალური სიგრძე). გამოიყენეთ ტრიგონომეტრიული თანაფარდობა მართკუთხა სამკუთხედში, რათა იპოვოთ კიბის დახრის კუთხე (α) ჰორიზონტალურ ზედაპირთან მიმართებით. შეაფასეთ, რამდენად მისაღებია მიღებული კუთხე. თუ თქვენი კუთხე ამ დიაპაზონს სცდება უსაფრთხო კუთხის სტანდარტებს, იმსჯელეთ შესაძლო კორექტირებებზე (მაგალითად, საფეხურის ზომების ან რაოდენობის შეცვლა). კიბის დახრილი ნაწილის სიგრძე (S): გამოთვალეთ კიბის დახრილი ნაწილის (ჰიპოტენუზის) რეალური სიგრძე (S). ამისთვის შეგიძლიათ გამოიყენოთ: პითაგორას თეორემა ან ტრიგონომეტრიული თანაფარდობები: (sin(α) ან cos(α)) პროექტის ვიზუალიზაცია: მოამზადეთ კიბის პროექტის მასშტაბირებული ნახაზი (გვერდითი ხედი). ნახაზზე მკაფიოდ დაიტანეთ შემდეგი ზომები და აღნიშვნები: საერთო სიმაღლე (H) საერთო ჰორიზონტალური სიგრძე (L) დახრილი ნაწილის სიგრძე (S) დახრის კუთხე (α) ერთი საფეხურის სიმაღლე (h) და სიღრმე (d) საფეხურების რაოდენობა (N) ნაშრომში ხაზგასმით წარმოადგინეთ მასალები (პროდუქტი): წერილობითი ანგარიში, რომელიც მოიცავს: თავდაპირველად არჩეული კიბის საერთო სიმაღლე (H). ინფორმაცია მოძიებული სტანდარტებისა და რეკომენდაციების შესახებ. საფეხურის სიმაღლისა (h) და სიღრმის (d) არჩევის დასაბუთება. ყველა ჩატარებული გამოთვლა დეტალურად (საფეხურების რაოდენობა, L, α, S), გამოყენებული ფორმულების მითითებით. ტრიგონომეტრიული ფუნქციების გამოყენების ახსნა-განმარტება თქვენს გამოთვლებში. დისკუსია კიბის დიზაინის უსაფრთხოებასა და კომფორტულობაზე (მაგ., მიღებული დახრის კუთხის შეფასება). შესაძლო გამოწვევები და მათი გადაჭრის გზები (მაგალითად, თუ თავდაპირველი გათვლებით კუთხე მიუღებელი აღმოჩნდა).   კიბის მასშტაბირებული ნახაზი (გვერდითი ხედი), ყველა საჭირო აღნიშვნით.   შეფასების კრიტერიუმები: ტრიგონომეტრიული ცნებებისა და თანაფარდობების გააზრება და კორექტული გამოყენება: რამდენად სწორად არის გამოყენებული სინუსი, კოსინუსი, ტანგენსი ან პითაგორას თეორემა. გამოთვლების სიზუსტე: არითმეტიკული და ტრიგონომეტრიული გამოთვლების სისწორე. პრობლემის გადაჭრის უნარი: ამოცანის პირობის გააზრება, ლოგიკური მსჯელობა და გადაწყვეტილების მიღება. დიზაინის არჩევანის დასაბუთება: რამდენად კარგად არის ახსნილი საფეხურის ზომების, დახრის კუთხის და სხვა პარამეტრების შერჩევა. უსაფრთხოებისა და კომფორტის სტანდარტების გათვალისწინება: რამდენად შეესაბამება დაპროექტებული კიბე ზოგად რეკომენდაციებს. წარმოდგენილი მასალის ხარისხი: ანგარიშის სტრუქტურირებულობა, სიცხადე, ლაკონიურობა და ნახაზის აკურატულობა, მასშტაბის დაცვა და ინფორმაციულობა. კვლევითი უნარები: საჭირო ინფორმაციის მოძიებისა და გამოყენების უნარი. დამატებითი მითითებები: შეგიძლიათ გამოიყენოთ დამხმარე რესურსები (სახელმძღვანელო, ინტერნეტი, პროგრამული უზრუნველყოფა კიბის ესკიზისათვის). იმუშავეთ ჯგუფურად. პრეზენტაციის დროს შეგიძლიათ გამოიყენოთ ვიზუალური მასალები.   წარმატებებს გისურვებთ!

აქტივობა 3. პრეზენტაცია და დისკუსია:

ბოლოს გაიმართა პრეზენტაცია და დისკუსია:

• თითოეულმა ჯგუფმა წარმოადგინა თავის მიერ შექმნილი დიზაინის ვარიანტები, გამოთვლები და დასკვნები.
• გაიმართა დისკუსია სხვადასხვა დიზაინის უპირატესობებსა და ნაკლოვანებებზე.

ერთმანეთს დაუსვეს ისეთი კითხვები, როგორიცაა:

• როგორ მოქმედებს საფეხურის სიმაღლისა და სიღრმის ცვლილება კიბის დახრის კუთხეზე?
• რომელი დიზაინი იქნება უფრო მოსახერხებელი ხანდაზმული ადამიანებისთვის ან ბავშვებისთვის?
• რა ფაქტორები უნდა გავითვალისწინოთ კიბის დიზაინის არჩევისას სივრცის შეზღუდვის შემთხვევაში? და სხვა.

აქტივობა 4. შეჯამება-შეფასება.

მოსწავლეებს ვთხოვე, მოკლედ გაეზიარებინათ თავიანთი შთაბეჭდილებები აქტივობის შესახებ 3-2-1 შეფასების ინსტრუმენტის გამოყენებით

მოსწავლეებს ძალიან მოეწონათ ზემოთ აღწერილი აქტივობა. ისინი ინტერესით ჩაერთნენ დავალების თითოეულ ეტაპში და წარმოადგინეს ძალიან საინტერესო პრეზენტაციები. მოსწავლეებმა არა მხოლოდ გაიაზრეს თეორიული ცნებები, არამედ განავითარეს პრაქტიკული უნარები, როგორიცაა პრობლემის გადაჭრა, მათემატიკური მოდელირება, სივრცითი აზროვნება და დიზაინის ოპტიმიზაცია.

აქტივობის განმავლობაში, მოსწავლეებმა შეძლეს:

• კიბის პარამეტრების ანალიზი და მათი გავლენის შეფასება უსაფრთხოებასა და კომფორტზე.
• სხვადასხვა დიზაინის ვარიანტის შექმნა და შედარება.
• არგუმენტირებული მსჯელობის საფუძველზე ოპტიმალური გადაწყვეტილების მიღება.
• ჯგუფური მუშაობისა და პრეზენტაციის უნარების განვითარება.

დავალებაზე მუშაობის პროცესში, მოსწავლეებმა გააცნობიერეს, რომ მათემატიკა არ არის აბსტრაქტული საგანი, არამედ მძლავრი ინსტრუმენტია რეალური სამყაროს პრობლემების გადასაჭრელად. ამ ტიპის აქტივობები ხელს უწყობს მოსწავლეების მოტივაციის ამაღლებას, მათში კრიტიკული აზროვნებისა და დამოუკიდებელი სწავლის უნარების განვითარებას.

ვფიქრობ, წინამდებარე გამოცდილება წარმატებით შეიძლება იქნას გამოყენებული მე-10 კლასის მათემატიკის გაკვეთილებზე, რაც ხელს შეუწყობს სწავლების ხარისხის გაუმჯობესებას და მოსწავლეების უფრო ეფექტურ მომზადებას თანამედროვე გამოწვევებისთვის.

გამოყენებული ლიტერატურა

1. ეროვნული სასწავლო გეგმა https://mes.gov.ge/content.php?id=3929&lang=geo
2. მათემატიკის გზამკვლევი მეათე კლასი. შედგენილი ქეთი ცერცვაძის მიერ,

ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/meate-klasi/

3. https://math.stackexchange.com/questions/4081984/solving-trigonometric-word-problems-with-limited-information
4. https://www.graitec.com/Help/PowerPack_for_Advance_Steel/En/Balanced_Stair_Ergonomics_-_Overview.htm