მოსწავლეთა მეცნიერული კვლევის უნარ-ჩვევების განვითარება ბიოლოგიის სწავლებისას

მეორე ნაწილი

გთავაზობთ კიდევ ერთ ექსპერიმენტს, რომელიც ხელს შეუწყობს მოსწავლეთა მეცნიერული უნარ-ჩვევების განვითარებას.

ეს ექსპერიმენტი თითქმის პირველის იდენტურია, თუმცა, გამოყენებული რესურსების თვალსაზრისით, უფრო მარტივი. ის კლასშიც შეიძლება ჩატარდეს რეფლექსიის ფაზაში და საშინაო დავალებადაც მიეცეს მოსწავლეებს – ეს მათ განუვითარებს თეორიული ცოდნის პრაქტიკაში გამოყენების უნარ-ჩვევებს.

ექსპერიმენტი: ალბათობის თეორია გენეტიკაში

თემა: მენდელის კანონების სტატისტიკური ხასიათი

წინარე ცოდნა და უნარ-ჩვევები: მოსწავლეებმა იციან მონოჰიბრიდული შეჯვარების არსი და დათიშვის კანონი. ამ კანონის თანახმად, მონოჰიბრიდული შეჯვარების დროს მიღებული პირველი თაობის ჰიბრიდების თვითდამტვერვის გზით ან ერთმანეთთან შეჯვარებით გამრავლებისას მეორე თაობაში გამოვლინდება რიგორც დომინანტური, ისე რეცესიული ნიშან-თვისება თანაფარდობით 3:1. მოსწავლეებმა იციან, რომ მენდელის კანონებს სტატისტიკური ხასიათი აქვს.

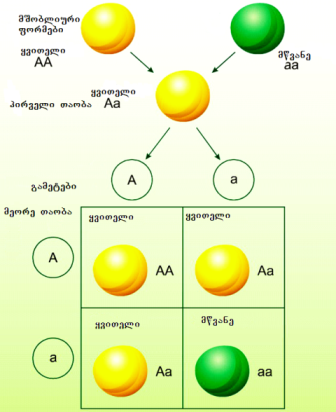
შეიძლება პენეტის ცხრილის გამოყენება გენოტიპური და ფენოტიპური დათიშვის თანაფარდობის დასადგენად.

კავშირი სტანდარტთან

კვლ.XI.2. მოსწავლეს შეუძლია კვლევითი პროცედურის განხორციელება/მონაცემების აღრიცხვა.

შედეგი თვალსაჩინოა, თუ მოსწავლე:

• იყენებს შესაბამის მასალას ან/და აღჭურვილობას და ატარებს დაგეგმილ ცდას უსაფრთხოების წესების დაცვით;

• აწარმოებს დაკვირვებას და/ან გაზომვებს, იღებს სარწმუნო მონაცემებს.

კვლ.XI.3. მოსწავლეს შეუძლია მონაცემთა წარმოდგენა სხვადასხვა საკომუნიკაციო საშუალების გამოყენებით.

შედეგი თვალსაჩინოა, თუ მოსწავლე:

• იყენებს სხვადასხვა ხერხს (დიაგრამებს, ცხრილებს, გრაფიკებს, სიებს) მონაცემთა წარმოსადგენად.

კვლ.XI.4.მოსწავლეს შეუძლია მონაცემთა ანალიზი და შეფასება.

შედეგი თვალსაჩინოა, თუ მოსწავლე:

• იყენებს დიაგრამებს, ცხრილებსა და გრაფიკებს მონაცემებს ან ცვლადებს შორის დამოკიდებულების აღსაწერად;

• აანალიზებს მონაცემებს (მაგ., საშუალო არითმეტიკული სიდიდის და საშუალოდან გადახრების დადგენა), საჭიროების შემთხვევაში, საკონტროლო ცდის შედეგების გათვალისწინებით, გამოიტანს დასკვნებს;

• განიხილავს, საკმარისია თუ არა მონაცემები (რაოდენობრივად და თვისებრივად) გამოთქმული ვარაუდის დასადასტურებლად ან დასკვნის გამოსატანად;

• ადარებს დასკვნებს გამოთქმულ ვარაუდს, განსხვავების შემთხვევაში ხსნის მიზეზებს.

ბიოლ.XI.6. მოსწავლეს შეუძლია, ჩამოაყალიბოს მემკვიდრეობითობის კანონები და იმსჯელოს ცვალებადობის ფორმებზე.

შედეგი თვალსაჩინოა, თუ მოსწავლე:

• მოიპოვებს ინფორმაციას და ადარებს მემკვიდრეობითობისა და ცვალებადობის მოქმედებას, მსჯელობს მათ ბიოლოგიურ მნიშვნელობაზე;

• გენეტიკური ამოცანების გადაჭრისას იყენებს მონაცემთა ანალიზს, სტატისტიკისა და ალბათობის თეორიის ელემენტებს.

სასწავლო მიზანი:

მოსწავლეები შეძლებენ:

• ჰიპოთეზის გამოთქმას;

• დაგეგმილი ცდის ჩატარებას;

• მონაცემების აღრიცხვას;

• მონაცემთა ცხრილის საშუალებით მონაცემების წარმოდგენას;

• მონაცემების ანალიზს სტატისტიკისა და ალბათობის თეორიის გამოყენებით;

• ანალიზის საფუძველზე დასკვნების გამოტანას;

• დასკვნების შედარებას გამოთქმულ ვარაუდთან;

• საკუთარი მონაცენების სხვებისთვის გაცვლა/გაზიარებას;

• მსჯელობას მენდელის კანონების სტატისტიკური ხასიათის შესახებ.

ექსპერიმენტის მიზანი: როგორ მოქმედებს ალბათობის კანონი გენების კომბინაციაზე

მასალა: 2 მწვანე და 2 ყვითელი მარკერი, პლასტმასის ჭიქა

პროცედურა

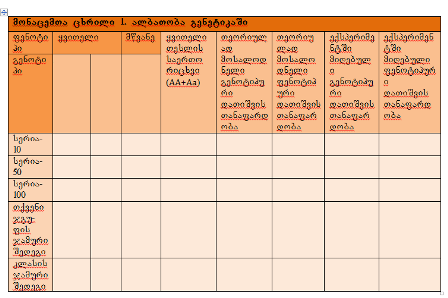
1. ცალკე ფურცელზე ან რვეულში მოამზადეთ ცხრილი მონაცემების აღრიცხვისთვის;

2.ბარდაში თესლის ყვითელი შეფერილობა (A) დომინირებს მწვანეზე (ა). გამოიყენეთ პენეტის ცხრილი და განსაზღვრეთ იმ ჰიბრიდების მოსალოდნელი გენოტიპი და ფენოტიპი, რომელთა მშობლებიც არიან ჰეტეროზიგოტურები (Aა) თესლის შეფერილობის მიხედვით;

3.ოთხივე მარკერი (ყვითელი და მწვანე) მოათავსეთ ჭიქაში. თითოეული მარკერი ასახავს ალელებს ჰეტეროზიგოტურ მცენარეებში;

4.ჭიქა შეანჯღრიეთ და თვალდახუჭულმა ამოიღეთ რომელიმე 2 მარკერი. 2 მარკერი ასახავს ალელების კომბინაციას კვერცხუჯრედისა და სპერმის შერწყმის დროს. ეს პროცედურა გაიმეორეთ 10-ჯერ და მარკერების – “ალელების” – კომბინაცია ჩაინიშნეთ მონაცემთა ცხრილში (ყოველი პროცედურის შემდეგ მარკერები ჭიქაში დააბრუნეთ);

5. მე-4 ნაბიჯი გაიმეორეთ ჯერ 50-ჯერ, შემდეგ – 100-ჯერ;

6. დათვალეთ თითოეული ტიპის გენოტიპი ყველა სერიისთვის;

7.მონაცემების გამოყენებით თითოეული სერიისათვის (10, 50 და 100) განსაზღვრეთ ყვითელი ფენოტიპების რაოდენობა;

8.მონაცემების გამოყენებით თითოეული სერიისათვის (10, 50 და 100) განსაზღვრეთ გენოტიპური და ფენოტიპური დათიშვის თანაფარდობა; დათიშვის თანაფარდობის გამოსათვლელად თითოეული გენოტიპის/ფენოტიპის რაოდენობის განმსაზღვრელი რიცხვი უნდა გავყოთ უმცირეს რიცხვზე და დავამრგვალოთ უახლოეს მთელ რიცხვამდე. მაგალითად, დავუშვათ, სერიისათვის 100, მიღებული გაქვთ ასეთი შედეგი: 23AA, 51Aა და 26აა; ამ შემთხვევისათვის გენოტიპური დათიშვის თანაფარდობა ასე იანგარიშება: 23/23=1, 51/23=2,2, 26/23=1,1. ე.ი. გენოტიპური დათიშვა ასეთია: 1AA: 2Aა: 1აა.

დაკვირვება

1. რომელი გენოტიპი იქნა მიღებული ყველაზე ხშირად?

2. როგორ გენოტიპურ და ფენოტიპურ დათიშვას მოელოდით?

3. როგორ გენოტიპურ და ფენოტიპურ დათიშვას მოელოდით 10-იან, 50-იან და 100-იან სერიაში?

ანალიზი და დასკვნა:

1. როგორ შეესაბამება ექსპერიმენტში მიღებული დათიშვის თანაფარდობა თეორიულად მოსალოდნელ დათიშვას?

2. რომელი სერიის დათიშვის მონაცემებია ყველაზე ახლოს თეორიულად მოსალოდნელ Dდათიშვის თანაფარდობასთან? ახსენით შედეგი.

3. როგორ აისახება ალბათობა თქვენი ექსპერიმენტის შედეგთან?

4. თქვენი ჯგუფის ჯამური შედეგები შეადარეთ კლასის ჯამურ შედეგებს. რომელ შემთხვევაშია გენოტიპებისა და ფენოტიპების რეალური თანაფარდობა უფრო ახლოს თეორიულად მოსალოდნელ თანაფარდობასთან? რატომ?

5. გამოთქვით ჰიპოთეზა, როგორ უნდა მიაღწიოთ, რომ რეალური შედეგი უფრო ახლოს იყოს თეორიულად მოსალოდნელ შედეგთან.

6. გამოიტანეთ დასკვნა, რატომ ატარებდა მენდელი ექსპერიმენტებს მრავალ ინდივიდზე და რატომ აგროვებდა დიდი რაოდენობის მონაცემებს.

რეკომენდაცია მასწავლებლებისთვის: თუ საშინაო დავალებად მიეცით, სასურველია, დავალების შესაფასებლად კლასი დაყოთ მცირე ჯგუფებად, სადაც ისინი გაუზიარებენ ერთმანეთს ცდის შედეგებს, მონაცემთა ცხრილში შეიტანენ თავიანთი ჯგუფის ჯამურ შედეგებს და პრეზენტაციის დროს თითოეული ჯგუფი თავის შედეგებს დააფიქსირებს თქვენ მიერ შედგენილ მონაცემთა ცხრილში. ამის შემდეგ კლასის ჯამური შედეგების განხილვა გაადვილდება.