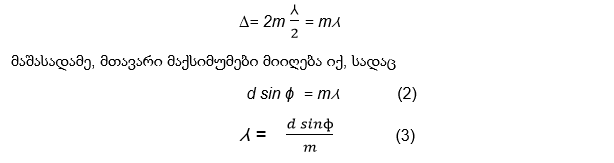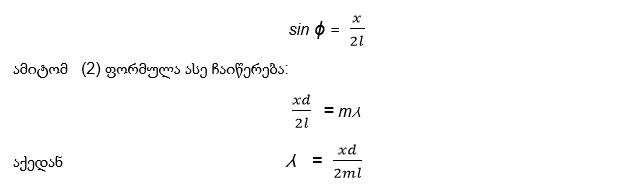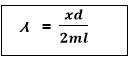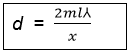თანამედროვე ფიზიკის თანახმად, სინათლე წარმოადგენს ელექტრომაგნიტურ ტალღას, რომელიც ვრცელდება სივრცეში და გადააქვს ენერგია. მას ახასიათებს ორმაგი ბუნება, ანუ კორპუსკულურ-ტალღური დუალიზმი. ერთი მხრივ, სინათლე არის ფოტონების ნაკადი. ფოტონი ელექტრომაგნიტური გამოსხივების კვანტია, გააჩნია გარკვეული (დისკრეტული) ენერგია და შეიძლება აღვწეროთ, როგორც ნაწილაკი. ფოტონის მიერ გადატანილი ენერგიის რაოდენობა განსაზღვრავს სინათლის ფერს. დაბალი ენერგიის მქონე ფოტონები აღიქმება წითლად. მაღალი ენერგიის მქონე ფოტონები კი იისფერად. მეორე მხრივ, სინათლეს ახასიათებს ისეთი თვისებები, რომელთა აღწერა შეუძლებელია მხოლოდ ნაწილაკური მოდელით, ასეთია სინათლის ტალღური გამოვლინება. ამ ორმაგი ბუნების ერთიანად აღქმა აძლევს მეცნიერებს საშუალებას, ახსნან სინათლის რთული თვისებები.
სინათლე გავრცელებისას ავლენს ტალღურ ბუნებას. ამის დამადასტურებელია სინათლის არეკვლა, გარდატეხა, დისპერსია, დიფრაქცია, ინტერფერენცია. გამოსხივებისა და შთანთქმის დროს კი იგი ხასიათდება კორპუსკულური თვისებებით. მისი ნაწილაკური ბუნების გამოვლენაა ფოტოელექტრული ეფექტი, კომპტონის გაფანტვა, შავი სხეულის გამოსხივება, სინათლის წნევა (ფოტონების იმპულსი).
სინათლის სიჩქარე ვაკუუმში C = 3.108 მ/წმ-ის ტოლია. მას ახასიათებენ ტალღის სიგრძით (λ) და სიხშირით (Ƴ). ამ სიდიდეებს შორის დამოკიდებულება ჩაიწერება შემდეგი ფორმულით:
C = λƳ
ხილული სინათლე შედგება სხვადასხვა ტალღის სიგრძის მონოქრომატული ტალღებისაგან. გახურებული სხეულების გამოსხივებაში (მაგალითად, ვარვარების ნათურის ძაფში) სხვადასხვა სიხშირის ტალღები უწყვეტად ავსებენ სინათლის მთელ დიაპაზონს. ასეთ გამოსხივებას უწოდებენ თეთრ სინათლეს.
მონოქრომატული ტალღების ერთობლიობა ქმნის სპექტრს. თეთრ სინათლეს აქვს უწყვეტი სპექტრი, ხოლო ისეთი წყაროს გამოსხივება, რომელშიც სინათლეს ატომები ასხივებენ, დისკრეტული სპექტრის ხასიათს ატარებს. სინათლის ასეთ თვისებებს სწავლობენ სპექტრული ხელსაწყოების საშუალებით.
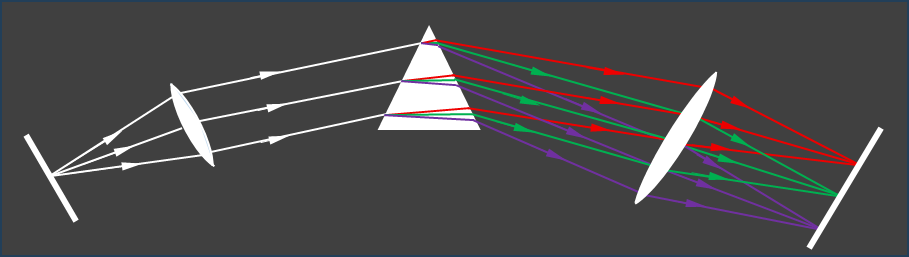
სინათლის ფერებად დასაშლელად, უმარტივეს სპექტრულ ხელსაწყოებში გამოიყენება პრიზმა. პრიზმის მოქმედება დამყარებულია დისპერსიის მოვლენაზე.
ვიწრო ხვრელიდან გამოსული სინათლის კონა ეცემა შემკრებ ლინზას. ლინზიდან გამოსული სინათლის პარალელური სხივები კი პრიზმას. დისპერსიის შედეგად განსხვავებული ტალღის სინათლის სხივები პრიზმიდან სხვადასხვა მიმართულებით გამოდიან. სხივებს წინ ხვდება მეორე შემკრები ლინზა. ამ ლინზის ფოკალურ სიბრტყეში მოთავსებულია ეკრანი ან ფოტოფირფიტა, რომელზეც მიიღება გამოსახულება. პრიზმა საწყისი მიმართულებიდან ყველაზე მეტად იისფერ სხივებს გადახრის, ყველაზე ნაკლებად კი – წითელს. თეთრი სინათლის სპექტრად დაშლის პირველი ცდა 1672 წელს ისააკ ნიუტონს ეკუთვნის.
დაბრკოლებების გარშემო ტალღების გავრცელების მოვლენას უწოდებენ დიფრაქციას. დიფრაქცია ახასიათებს ბგერებს, ელექტრომაგნიტურ ტალღებს – ხილულ სინათლეს, რენტგენისა და გამა სხივებს, უმცირესი ზომის ნაწილაკებს, როგორიცაა – ატომები, ნეიტრონები, ელექტრონები. დიფრაქცია არის დაბრკოლების გამო, ენერგიის ცვლილების გარეშე, ტალღების წრფივი გავრცელებიდან გადახრა.
დიფრაქციული მესერი წარმოადგენს გავრცელებული ტალღის მეორად წყაროს. დიფრაქციის ერთ-ერთი მთავარი თვისებაა ის, რომ ამ მოვლენის დროს მკვეთრი ჩრდილები არ წარმოიქმნება. როცა სინათლე დიფრაქციას განიცდის, ტალღები ერთმანეთს ებმის. თუ ისინი ერთმანეთს ემატება, ჩნდება ნათელი ზოლი; თუ თრგუნავს – ბნელი ზოლი. ამ მოვლენას კი ეწოდება ინტერფერენცია. სწორედ ინტერფერენციის შედეგად ვხედავთ ეკრანზე ნათელი და ბნელი ზოლების ერთობლიობას, რომლებიც ერთმანეთისგან თანაბრადაა დაშორებული. ამ ზოლების დაშორებით შეგვიძლია გამოვთვალოთ სინათლის ტალღის სიგრძე.
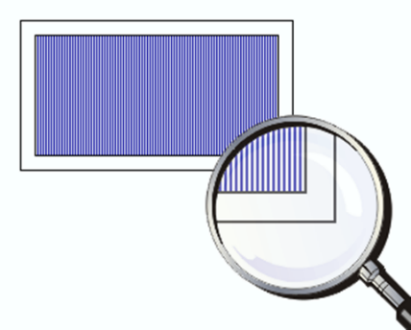
დიფრაქციისა და ინტერფერენციის ეფექტები შეგვიძლია დავინახოთ ბუნებაში. ამის მაგალითებია ობობას ქსელის ფერადი ნათება, დნმ-ის სპირალური ნიმუშები და ბუმბულის მიკროსქემებში გამოხატული ტალღური სტრუქტურები. მწერების სხეულსა და ფრინველების ბუმბულს მიკროსკოპულ დონეზე აქვს წესრიგი, სადაც ფორმები მეორდება, რაც სინათლის დაცემისას ქმნის დიფრაქციულ სურათს. წარმოქმნილი დიფრაქციული ზოლების დაშორების გაზომვით შეგვიძლია, გამოვთვალოთ სინათლის ტალღის სიგრძე და უკეთ გავიგოთ მისი ტალღური ბუნება. სურათზე ჩანს გადიდებული ფარშევანგის ბუმბული.
ობობას ქსელი მზის სხივზე ფერადად ელვარებს. ზოგიერთი ანალიზის თანახმად, ობობას ქსელში დანახული ფერები, დიფრაქციით არის განპირობებული. მისი ძალიან თხელი ძაფები სინათლისთვის დაბრკოლებას წარმოადგენს, რაც იწვევს ტალღების გაფანტვას და ქმნის დიფრაქციულ სურათს. სხვადასხვა სიგრძის ტალღები სხვადასხვა მიმართულებით ვრცელდება და ჩნდება ფერადი ელვარება.
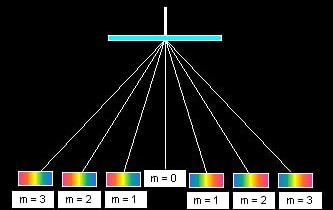
თეთრი სინათლის წყაროს შემთხვევაში, დიფრაქციული მესერი წარმოქმნის სპექტრების სერიას, რომელშიც თითოეული მონოქრომატული სხივი გარდატეხის კუთხეების მიხედვით გადანაწილდება. უმოკლესი (იისფერი) ტალღის სიგრძის სინათლე გარდატყდება ყველაზე დიდი კუთხით, ხოლო ყველაზე გრძელი (წითელი) ტალღები – უმცირესი კუთხით. ეს თვისება საშუალებას გვაძლევს სპექტროსკოპიული ანალიზით ზუსტად გამოვთვალოთ სხვადასხვა ფერის სინათლის ტალღის სიგრძე და შევისწავლოთ თეთრი სინათლის სტრუქტურა.
დიფრაქციული მესერს თუ დაეცემა ერთი ტალღის სიგრძის (მონოქრომატული) სინათლე, მაგალითად ლაზერიდან, მაშინ წარმოიქმნება მკვეთრი ხაზების სერია, სპექტრის თითოეულ რიგზე თითო ხაზი.
ლაზერის სხივი მონოქრომატულია. ის შეიძლება იყოს სხვადასხვა ფერის – წითელი, მწვანე, ლურჯი ან იისფერი. იისფერი ლაზერი ნაკლებადაა გავრცელებული, ზოგადად, სპეციალურ ლაბორატორიებში ან მაღალტექნოლოგიურ აპლიკაციებში გამოიყენება. როდესაც ლაზერის მონოქრომატული სხივი ეცემა დიფრაქციულ მესერს, ეკრანზე წარმოიქმნება მკვეთრი, ცალ–ცალკე განლაგებული ხაზების სერია. თითოეული ხაზის პოზიცია პირდაპირ არის დამოკიდებული სინათლის ტალღის სიგრძეზე. ეს მოვლენა საშუალებას გვაძლევს ზუსტად აღვწეროთ და შევისწავლოთ მონოქრომატული სხივების დიფრაქციულ მესერზე განაწილება.
მაღალი კლასის სპექტრულ ხელსაწყოებში პრიზმის ნაცვლად იყენებენ დიფრაქციულ მესერს. დიფრაქციული მესერი არის ფიზიკური ხელსაწყო, რომელიც წარმოადგენს გამჭვირვალე ან ამრეკლ ზედაპირზე დატანილ, ერთმანეთისგან ერთნაირი მანძილით დაშორებულ, დიდი რაოდენობის ტოლი სიგანის პარალელური შტრიხების ერთობლიობას. დიფრაქციული მესერი მზადდება სპეციალური დამყოფი მანქანით, რომელიც მინის ფირფიტაზე პარალელურ შტრიხებს (განაკაწრებს) ხაზავს. განაკაწრების რიცხვი 1მმ-ზე ხშირად რამდენიმე ათასს აღწევს. სინათლის დიფრაქციის შედეგად, მესერზე წარმოიქმნება სპექტრი – სინათლის ინტენსივობების მაქსიმუმებისა და მინიმუმების ერთობლიობა.
დიფრაქციულ მესრად კომპაქტდისკის ან ძველი გრამოფონის ფირფიტის ნაწილიც შეიძლება გამოვიყენოთ. თუმცა, მინის პრიზმისგან განსხვავებით, ამ შემთხვევაში გარდატეხა არ ხდება. ეფექტი წარმოიქმნება დიფრაქციულ ბადეზე ამოტვიფრული ვიწრო ხაზებით გადაცემული ან არეკლილი სინათლის დიფრაქციიდან.
CD ან DVD დისკის ტრეკები ამრეკლავი დიფრაქციული მესრის როლს ასრულებს. ამრეკლავ დიფრაქციულ ბადეს იმავე ეფექტის წარმოქმნა შეუძლია. დიფრაქციული ტალღების ამ დაჯგუფებით წარმოქმნილი სხივი, რომელთაგან თითოეული სხვადასხვა ნაპრალიდან მოდის, ერთიანდება და ქმნის ტალღის ფრონტს, რომელიც იმავე მიმართულებით მოძრაობს, როგორც საწყისი შემომავალი სინათლის სხივი. ამ სხივს ჩვეულებრივ ცენტრალურ მაქსიმუმს უწოდებენ.
განვიხილოთ დიფრაქციული მესრის მოქმედების პრინციპი. ვთქვათ, მესრის ხვრელებს შორის მანძილი არის d. ამ მანძილს მესრის პერიოდი ეწოდება (ან მესრის მუდმივა). თუ დიფრაქციულ მესერს ეცემა სინათლის პარალელური კონა, ანუ ბრტყელი ტალღა, მაშინ მესრის თითოეული ხვრელი შეგვიძლია განვიხილოთ, როგორც დამოუკიდებელი წყარო, რომელიც სინათლეს ასხივებს ყველა მიმართულებით. ეს წყაროები იქნებიან კოჰერენტული, რადგან წარმოშობილი არიან ერთი ტალღისაგან.
თითოეული ხვრელი ქმნის საკუთარ დიფრაქციულ სურათს. ეს სურათები არიან ერთმანეთის იდენტური. მათი ზედდების შედეგად მიიღება გაცილებით რთული სურათი, რომელიც შეიცავს მთავარ მაქსიმუმებსა და მინიმუმებს; აგრეთვე დამატებით მაქსიმუმებსა და მინიმუმებს.
დიფრაქციული მესრის საშუალებით შესაძლებელია ტალღის სიგრძის დიდი სიზუსტით გაზომვა. თუ მესრის d პერიოდი ცნობილია, მაშინ ტალღის სიგრძის განსაზღვრა m-ური რიგის სპექტრში არჩეული ხაზის მიმართულების შესაბამისი ɸm კუთხის გაზომვამდე დაიყვანება. პრაქტიკაში ჩვეულებრივ გამოიყენება პირველი და მეორე რიგის სპექტრები.
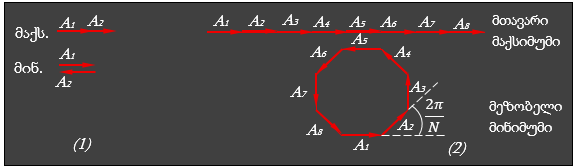
თუ საკვლევი გამოსხივების სპექტრში ორი სპექტრული ხაზია λ1 და λ2 ტალღის სიგრძეებით, მაშინ მესერს ყოველ სპექტრულ რიგში (გარდა m = 0) შეუძლია ერთი ტალღის მეორისაგან განცალკევება.
- – ორი ტალღის ინტერფერენცია
- – N ტალღის ინტერფერენცია ( N= 8)
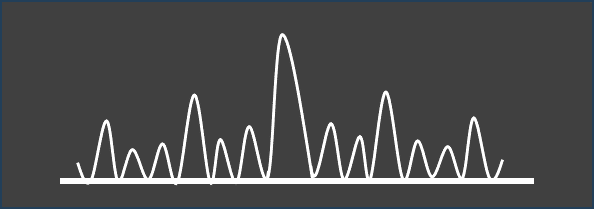
დიფრაქციული მესრის საშუალებით ეკრანზე მიღებული გამოსახულება მეორადი ტალღების ინტერფერენციის შედეგს წარმოადგენს.
ეკრანზე ინტერფერენციული მაქსიმუმის დასაკვირვებლად, მეზობელი ხვრელებიდან გამოსულ ტალღებს შორის სვლათა სხვაობა Δ ტალღის სიგრძის მთელი რიცხვის ტოლი უნდა იყოს:
Δ = d sin ɸm = mλ ( m = 0, ±1, ±2, … )
აქ d – მესრის პერიოდია, m – მთელი რიცხვი, რომელსაც დიფრაქციული რიგის მაქსიმუმს უწოდებენ. ეკრანის იმ წერტილებში, რომლებშიც ეს პირობა სრულდება, განთავსებულია ე.წ. დიფრაქციული სურათის მთავარი მაქსიმუმები.
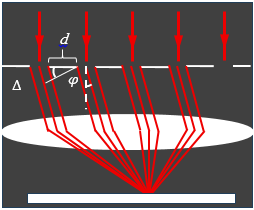
მთავარი მაქსიმუმები მიიღება იქ, სადაც ხვრელები აძლიერებენ ერთმანეთის მოქმედებას. დავადგინოთ მთავარი მაქსიმუმების მიღების პირობა. ვთქვათ, დიფრაქციის შედეგად სხივები განიცდიან ɸ კუთხით გადახრას.
ნახაზიდან ჩანს, რომ მეზობელი ხვრელებიდან გამოსულ ტალღებს შორის წარმოიშობა სვლათა სხვაობა ∆:
∆= d sin ɸ (1)
სადაც d დიფრაქციული მესრის პერიოდია.
ტალღები გააძლიერებენ ერთმანეთს, თუ მათ შორის შორის სვლათა სხვაობა ლუწი ნახევარტალღის ჯერადია, ე.ი.
მთავარ მაქსიმუმებს შორის მოთავსებულია დამატებითი მაქსიმუმები და მინიმუმები. მათი რიცხვი განისაზღვრება დიფრაქციულ მესერში ხვრელთა რაოდენობით. კერძოდ, თუ მესერი შეიცავს N ხვრელს, მაშინ მიიღება (N-2) დამატებითი მაქსიმუმი და (N-1) დამატებითი მინიმუმი.
მოცემულ ნახაზზე ნაჩვენებია შემთხვევა, როდესაც N=4.
(3) ფორმულის გამოყენებით შეგვიძლია განვსაზღვროთ სინათლის ტალღის სიგრძე, თუ ცნობილია მესრის პერიოდი და მიმართულება (ɸ), ერთ-ერთ მთავარ მაქსიმუმზე. უმჯობესი იქნება, დავადგინოთ ისეთი ფორმულა, რომელში შემავალი სიდიდეები პრაქტიკულად უფრო ადვილად გამოსათვლელი იქნება.
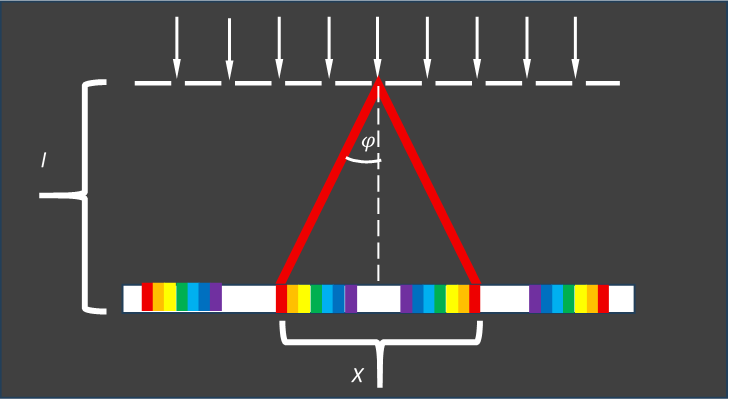
განვიხილოთ შედარებით მარტივი ნახაზი:
l არის მანძილი მესრიდან ეკრანამდე. X არის მანძილი ორ წითელ ზოლს შორის m – ური რიგის სპექტრში (შესაძლებელია წითლის ნაცვლად სხვა ფერის შერჩევა). როგორც ნახაზიდან ჩანს,
მიღებული ფორმულა საფუძვლად უდევს სინათლის ტალღის სიგრძის განსაზღვრას დიფრაქციული მესრის საშუალებით. სადაც
- ⅄ არის სინათლის ტალღის სიგრძე;
- მანძილი ეკრანზე მიღებულ ორ იდენტურ ფერს შორის;
- არის დიფრაქციული მესრის მუდმივა ( ეს მონაცემი აწერია მესერს);
- სპექტრის ნომერი (1,2,3…);
- მანძილი დიფრაქციულ მესერსა და ეკრანს შორის.
ექსპერიმენტისთვის საჭირო ხელსაწყოები
- საპროექციო აპარატი (ან ლაზერი);
- სპეციალური ეკრანი სახაზავით;
- დიფრაქციული მესერი;
- დიაფრაგმა.
ექსპერიმენტის მსვლელობა
შენიშვნა: ლაზერის გამოყენების შემთხვევაში ეკრანზე მიიღება მხოლოდ ერთი ფერის სპექტრი, რადგან ლაზერით მიღებული მონოქრომატული სინათლე ფერებად არ იშლება.
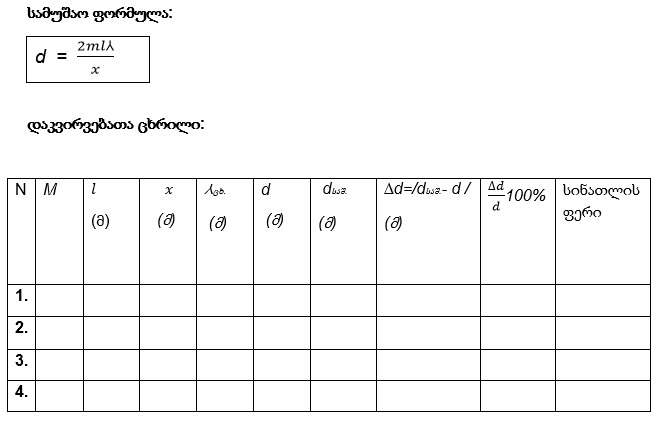
სამუშაო ფორმულა:
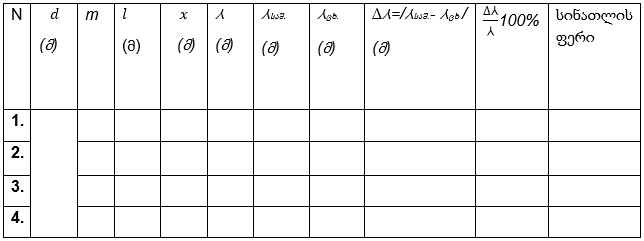
დაკვირვებათა ცხრილი:
თუ ექსპერიმენტის ჩასატარებლად, დიფრაქციული მესრის ნაცვლად ვიყენებთ კომპაქტდისკის ან ძველი გრამოფონის ფირფიტის ნაწილს, საჭირო გახდება სინათლის ტალღის სიგრძე ჩავთვალოთ ცნობილ სიდიდედ (გამოვიყენოთ ცხრილის მონაცემები) და გამოვთვალოთ დიფრაქციული მესრის მუდმივა. ამ შემთხვევაში უნდა გამოვიყენოთ სხვა სამუშაო ფორმულა და შესაბამისი ცხრილი.
სამუშაო ფორმულა:
დაკვირვებათა ცხრილი:
დიფრაქციის მოვლენაზე ჩატარებული ექსპერიმენტები საშუალებას გვაძლევს, დავაკვირდეთ სინათლის ტალღურ ბუნებას და გამოვთვალოთ სინათლის ტალღის სიგრძე და დიფრაქციული მესრის მუდმივა. ასეთი პრაქტიკული სამუშაოები ეხმარება თეორიული ცოდნის პრაქტიკაში ტრანსფერს და აღრმავებს წარმოდგენას სინათლის ფიზიკურ თვისებებზე.
გამოყენებული ლიტერატურა:
ქუთაისის ტექნიკური უნივერსიტეტი –
„ლაბორატორიული პრაქტიკუმი ფიზიკაში – ოპტიკა“
რ. აკობიძე, თ. ბარდაველიძე, ნ. ჩხეიძე