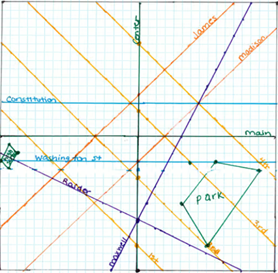
პარალელური და მართობული წრფეების განტოლებების თემა ერთ-ერთი ფუნდამენტური საკითხია, რომელიც ალგებრისა და გეომეტრიის გადაკვეთაზე დგას. ამ კონცეფციების გაგება აუცილებელია არა მხოლოდ მათემატიკაში შემდგომი წინსვლისთვის, არამედ მათი პრაქტიკული გამოყენების დანახვისთვისაც ინჟინერიაში, ფიზიკასა და ყოველდღიურ ცხოვრებაში.
ქვემოთ გაგიზიარებთ მე-8 კლასში ჩატარებულ გაკვეთილზე გამოყენებულ კვლევაზე დაფუძნებული სწავლების მეთოდს. მოსწავლეებმა დამოუკიდებლად აღმოაჩინეს წრფეების დახრილობებს შორის არსებული ძირითადი პრინციპები, რამაც ხელი შეუწყო ცნებების უფრო ღრმა გაგება-გააზრებას.
თემა:
დამოკიდებულება, ფუნქცია, გრაფიკი; ანალიზური გეომეტრია; გარდაქმნები
საკითხთა კლასტერი:
- ფუნქცია
- წრფივი ფუნქცია (წრფივი ფუნქციის წარმოდგენა სტანდარტული და კუთხური კოეფიციენტის ფორმით)
- გეომეტრიული გადაქმნები
სამიზნე ცნებები:
◦ მათემატიკური მოდელი: რეალური ვითარების (ქალაქის გეგმა) აღწერა მათემატიკური განტოლებებით; მათემატიკური შედეგების (დახრილობის მნიშვნელობები) გადმოტანა რეალურ კონტექსტში (პარალელურობა, მართობულობა)
◦ კანონზომიერება: წრფეების დახრილობებს შორის არსებული კანონზომიერების (თანაბარი დახრილობა, ნამრავლი: -1) გამოვლენა; მიზეზშედეგობრივი კავშირების გაგება
◦ ლოგიკა: დასკვნის გამოტანა და მისი დასაბუთება; ფაქტებზე დაყრდნობით დასკვნების ჩამოყალიბება; კრიტიკული აზროვნება
სტანდარტის მიხედვით მისაღწევი შედეგები
მოსწავლემ უნდა შეძლოს:
- სიტუაციის მოდელირება ვერბალურად მოცემული ამოცანის პირობის შესაბამისად და პრობლემის გადაჭრა (მათ. საბ. 1, 2, 3, 5, 7, 9, 10);
- ფუნქციებისა და მათი თვისებების გამოყენება სიდიდეებს შორის დამოკიდებულების აღსაწერად და გამოსაკვლევად (მათ. საბ. 1, 2, 3, 8, 9, 10);
- რეალურ ცხოვრებასა და სამყაროში მიმდინარე მოვლენების აღწერა გეომეტრიული ობიექტების მეშვეობით (მათ. საბ. 7);
- ტექნოლოგიების გამოყენებით ნახაზის აგება და პრობლემის გადაჭრა (მათ. საბ. 11).
გაკვეთილის მიზანი: მოსწავლეებმა კვლევის საფუძველზე თავად აღმოაჩინონ პარალელური და მართობული წრფეების კუთხურ კოეფიციენტებს (დახრილობებს) შორის არსებული ურთიერთკავშირი.
სასწავლო რესურსები:
- კომპიუტერები/ ტაბლეტები ინტერნეტთან წვდომით
- ონლაინ გრაფიკული კალკულატორი (მაგალითად, Desmos ან GeoGebra)
- სამუშაო ფურცლები თითოეული ჯგუფისთვის
- სახაზავი და ფანქრები (არასავალდებულო, მაგრამ გამოსადეგი)
გაკვეთილის მსვლელობა
გაკვეთილი დავიწყე მოკლე ინტერაქციული დისკუსიით, რათა მოსწავლეებმა გაიხსენონ უკვე ნასწავლი მასალა.
აქტივობა 1: წინარე ცოდნის გააქტიურება
- მთელი კლასის დისკუსია. საბაზისო ცოდნის გასახსენებლად მოსწავლეებს დავუსვი კითხვები:
- რა არის წრფის კუთხური კოეფიციენტი/ დახრა? რას გვეუბნება ის წრფის შესახებ?
- რა არის y=mx+b განტოლებაში m და b?
- რა შემთხვევაშია წრფის კუთხური კოეფიციენტი განუსაზღვრელი?
- როგორ შეიძლება გამოვთვალოთ დახრილობა, თუ წრფეზე ორი წერტილი გვაქვს?
აქტივობა 2: პარალელური წრფეების აღმოჩენა
კლასი დავყავი 3-4 მოსწავლისგან შემდგარ ჯგუფებად. თითოეულ ჯგუფს მივეცი დავალება Desmos-ში ან GeoGebra-ში სამუშაოდ, ასევე – სამუშაო ფურცელი, რომელზეც მოცემული იყო წრფეების რამდენიმე წყვილი. მათ უნდა შეესრულებინათ სამუშო, დაკვირვებოდნენ შედეგებს და დამოუკიდებლად გამოეტანათ დასკვნები.
დავალების ფურცელი (ერთი ჯგუფის მაგალითზე):
- მოცემულია წრფეთა წყვილები:
- y=2x+1 და y=2x−3
- y=−0.5x+4 და y=−0.5x+2
- y=31x−2 და y=31x+5
- y=4x+1 და y=−4x+1
- y=x+2 და y=x−3
- კვლევის ეტაპები:
- თითოეული წყვილი შეიყვანეთ გრაფიკულ კალკულატორში.
- დააკვირდით, როგორ გამოიყურება წრფეები.
- შეავსეთ სამუშაო ფურცელი: „კვეთენ თუ არა წრფეები ერთმანეთს?“ და „რა დახრილობები აქვთ მათ?“
| წრფეთა წყვილები | წრფე 1-ის განტოლება | წრფე 2-ის განტოლება | დახრილობა (m1) | დახრილობა (m1) | იკვეთებიან თუ არა წრფეები? (კი/არა) |
| წყვილი 1 | y=2x+3 | y=2x−1 | |||
| წყვილი 2 | y=−0,5x+4 | y=−0,5x+2 | |||
| წყვილი 3 | y=31x−2 | y=31x+5 | |||
| წყვილი 4 | y=4x+1 | y=−4x+1 | |||
| წყვილი 5 | y=x+2 | y=x−3 |
- ცხრილზე დაკვირვების შედეგად გააანალიზეთ თქვენი პასუხები. რა ურთიერთდამოკიდებულებას ამჩნევთ იმ წრფეების დახრილობებს შორის, რომლებიც არასდროს კვეთენ ერთმანეთს?
დაწერეთ თქვენი დასკვნა აქ:
- პრეზენტაციისთვის მომზადება
ანალიზი და დასკვნა: როდესაც ჯგუფებმა დაასრულეს, ვთხოვე თითოეულ ჯგუფს, გაეზიარებინა კლასისთვის თავისი დაკვირვება. მე ფასილიტაცია გავუწიე დისკუსიას, მოსწავლეებმა კი თავად გამოიტანეს დასკვნა, რომ პარალელურ წრფეებს ერთნაირი კუთხური კოეფიციენტი/ დახრა აქვთ.
აქტივობა 3: მართობული წრფეების აღმოჩენა (15 წუთი)
მოსწავლეებმა ჩაატარეს ანალოგიური კვლევა, ოღონდ ამჯერად მართობული წრფეებისთვის.
ჯგუფური დავალება (დავალების ახალი ფურცელი წრფეების სხვა წყვილებით ერთი ჯგუფის მაგალითზე)
- მოცემულია წრფეთა წყვილები:
- y=2x+1 და y=−21x−3
- y=43x−2 და y=−34x+5
- y=−3x+4 და y=31x−1
- კვლევის ეტაპები:
- თითოეული წყვილი შეიყვანეთ გრაფიკულ კალკულატორში.
- დააკვირდით, როგორ იკვეთებიან წრფეები. შეგიძლიათ, გამოიყენოთ კუთხის საზომი ინსტრუმენტი (ხელმისაწვდომია Desmos-ში) კუთხის გასაზომად.
- შეავსეთ სამუშაო ფურცელი: „რა კუთხით იკვეთებიან წრფეები?“ და „რა დახრილობები აქვთ მათ?“ ასევე გამოთვალეთ ამ დახრილობების ნამრავლი.
| წრფეთა წყვილები | წრფე 1-ის განტოლება | წრფე 2-ის განტოლება | დახრილობა (m1) | დახრილობა (m1) | დახრილობების ნამრავლი (m1⋅ m₂) | იკვეთებიან თუ არა წრფეები მართი კუთხით? (კი/არა) |
| წყვილი 1 | y=2x+1 | y=−0,5x−3 | ||||
| წყვილი 2 | y=3/4x−2 | y=−4/3x+5 | ||||
| წყვილი 3 | y=−3x+4 | y=1/3x−1 | ||||
| წყვილი 4 | y=x+2 | y=−x−3 | ||||
| წყვილი 5 | y=5x+3 | y=−1/5x+2 |
- ცხრილზე დაკვირვების შედეგად გააანალიზეთ თქვენი პასუხები. რა ურთიერთდამოკიდებულებას ამჩნევთ იმ წრფეების დახრილობებს შორის, რომლებიც ერთმანეთს მართი კუთხით კვეთენ? გამოიტანეთ დასკვნა.
- დაწერეთ თქვენი დასკვნა აქ:
- პრეზენტაციისთვის მომზადება
ანალიზი და დასკვნა: როდესაც ჯგუფებმა დაასრულეს მუშაობა, ვთხოვე თითოეულ ჯგუფს, გაეზიარებინა კლასისთვის თავისი დაკვირვება. დისკუსიის ფასილიტაციით მოსწავლეებმა თავად გამოიტანეს დასკვნა, რომ მართობული წრფეების კუთხური კოეფიციენტების ნამრავლი ყოველთვის -1-ის ტოლია. ასევე დავეხმარე მათ, აღმოაჩინათ შებრუნებული და საპირისპირო ცნებები.
ეს სამუშაო ფურცლები მოსწავლეებს დაეხმარა, გაეაზრებინათ მთელი კვლევის პროცესი – მონაცემების შეგროვებიდან (დახაზვა და დაკვირვება) დასკვნების გამოტანამდე (კანონზომიერების აღმოჩენა და წესების ფორმირება).
აქტივობა 4: შეჯამება და პრობლემის გადაჭრა
- მთელი კლასის აქტივობა: მოსწავლეებს დავუსვი კითხვები, მივეცი სავარჯიშოები, რომლებიც მოითხოვს ზემოთ „მიგნებული“ ცოდნის გამოყენებას.
- მოცემულია წრფე, რომლის განტოლებაა y=5x+2. როგორი იქნება პარალელური წრფის დახრილობა?
- მოცემულია წრფე, რომლის დახრილობაა 2/3. როგორი იქნება მართობული წრფის დახრილობა?
- პრაქტიკული ამოცანები სწრაფი წერისთვის: მივეცი მოსწავლეებს ინდივიდუალურად შესასრულებელი ამოცანების ბარათები:
- იპოვეთ განტოლება წრფისთვის, რომელიც გაივლის წერტილზე (4,−1) და პარალელურია წრფისა y=3x+5.
- არის თუ არა წრფეები y=2x+7 და y=−1/2x−1 მართობული და რატომ?
აქტივობა 5: რეალური სამყაროს კავშირები
გაკვეთილის ბოლოს მოსწავლეებს მივეცი კომპლექსური საშინაო დავალება, რომლის შესრულებასაც დასჭირდა 2-3 გაკვეთილი. ამ ხნის განმავლობაში მათთან ერთად ვიმუშავე მოცემულ თემაზე პროცედურული ცოდნის გასამდიდრებლად. იმავდროულად, ვაძლევდი განმავითარებელ შეფასებებს დავალებაზე მუშაობის ამა თუ იმ ეტაპზე. ამ კომპლექსური დავალების არსი ის არის, რომ მოსწავლეები ქმნიან პროდუქტს, რომელშიც თავიანთ ცოდნასა და უნარებს ასახავენ.
| კომპლექსური დავალება: ქალაქის რუკის შექმნა
საკვანძო შეკითხვა: როგორ შეიძლება გამოვიყენოთ წრფეების განტოლებები ქუჩებს შორის ურთიერთობის აღსაწერად და ქალაქის გეგმის შესადგენად? დავალების აღწერა:
თქვენი საბოლოო პროდუქტი უნდა იყოს:
დავალების ეტაპები: 1. დაგეგმვა:
პროდუქტის შეფასება: თქვენი დავალება შეფასდება შემდეგი კრიტერიუმებით:
|
მოსწავლეები აქტიურად მონაწილეობდნენ სასწავლო პროცესში. მათ მხოლოდ კი არ შეიძინეს პროცედურული ცოდნა, არამედ გაიგეს მისი არსი და ისწავლეს პრაქტიკული გამოყენებაც. იკვლიეს, გააანალიზეს, თავად მიაგნეს კანონზომიერებებს და დამოუკიდებლად გამოიტანეს დასკვნები. განუვითარდათ კვლევისა და ანალიზის, არგუმენტირებისა და დასაბუთების, ცოდნის პრაქტიკული გამოყენების უნარები.
გამოყენებული ლიტერატურა:
- ეროვნული სასწავლო გეგმა
https://mes.gov.ge/content.php?id=3929&lang=geo
- მათემატიკის გზამკვლევი მერვე კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/merve-klasi/
- https://math.libretexts.org/Bookshelves/Applied_Mathematics/Developmental_Math_(NROC)/13%3A_Graphing/13.02%3A_Slope_and_Writing_the_Equation_of_a_Line/13.2.03%3A_Parallel_and_Perpendicular_Lines
- https://www.teacherspayteachers.com/Product/Parallel-and-Perpendicular-City-Activity-3514871
