ცენტრალური ტენდენციის საზომი არის სტატისტიკური მნიშვნელობა, რომელიც აღწერს მონაცემთა განლაგებას ცენტრის მიმართ. საშუალო, მედიანა და მოდა ცენტრალური ტენდენციის საზომებია, გამოიყენება მოცემული მონაცემთა ნაკრების სხვადასხვა პარამეტრების დასადგენად და იძლევა მნიშვნელოვან დასკვნას შესწავლილი მონაცემების შესახებ, გვეხმარება მომავალი მოვლენებისა და ქცევების შესახებ პროგნოზების გასაკეთებლად. სტატისტიკა გამოიყენება ნებისმიერი ტიპის მონაცემების შესასწავლად, იგი ჩვენი ცხოვრების განუყოფელი ნაწილია, ყველგან არის და გვეხმარება ჩვენს ირგვლივ არსებული სამყაროს გაგებაში.
გიზიარებთ საშუალოს, მედიანისა და მოდის გამოყენების კონტექსტურ მაგალითებს მე-6 კლასელთათვის
თემა: მონაცემი, მონაცემთა ანალიზი. (მონაცემთა მოწესრიგება და ინტერპრეტაცია)
სამიზნე ცნება/ ქვეცნებები:
მათემატიკური მოდელი: მონაცემთა საშულო, მედიანა, მოდა
კანონზომიერება: რიცხვითი მახასიათებლების პოვნა; შერჩევა (ეფექტური მეთოდის შერჩევა)
ლოგიკა: კლასიფიკაცია (მონაცემთა კლასიფიკაცია) მსჯელობა/ ანალიზი
საკითხთა კლასტერი: მონაცემთა ანალიზი. მოდა, მედიანა, საშუალო
საკვანძო შეკითხვა: როგორ გვეხმარება მონაცემთა ორგანიზებისა და დამუშავების ხერხები საკვლევი საკითხების შესახებ დასკვნის გაკეთებაში?
მიზანი: მოსწავლეებმა უნდა შეძლონ მათემატიკური ცნებების (მოდა, მედეანა, საშუალო) გაგება და მათი გამოყენება ცხოვრებისეულ სიტუაციებში; ლოგიკური მსჯელობა თავიანთი პასუხების ასახსნელად, მსჯელობის შეფასება და ინტერპრეტირება.
სტანდარტის მიხედვით მისაღწევი შედეგები:
თემის ფარგლებში შედეგების მიღწევის ინდიკატორები სამიზნე ცნებების მიხედვით:
მათემატიკური მოდელი, კანონზომიერება, ლოგიკა – მოსწავლემ უნდა შეძლოს:
- საკითხის შესწავლასთან დაკავშირებით საკვლევი კითხვის ფორმულირება, რომელზე პასუხის გასაცემად საჭიროა მოწესრიგება; საკვლევი კითხვის განსხვავება არასაკვლევი კითხვისგან
- მონაცემთა განაწილების ძირითადი მახასიათებლების (მონაცემთა საშუალო, მედიანა, მოდა) მოძებნა;
- მონაცემთა ანალიზი და საკვლევ კითხვაზე არგუმენტირებული პასუხის გაცემა;
- მონაცემების ანალიზის საფუძველზე ინფორმირებული გადაწყვეტილების მიღება, ან სავარაუდო პროგნოზის გაკეთება;
გთავაზობთ თემის ფარგლებში განცორციელებულ რამდენიმე საინტერესო აქტივობას, რომელიც ჩემს მოსწავლეებს ძალიან მოეწონათ, სიამოვნებით იყვნენ ჩართულნი სწავლების პროცესში, რამაც ხელი შეუწყო ცნებების კონცეპტუალურ გაგებას.
აქტივობა1. წინარე ცოდნის გააქტიურება.
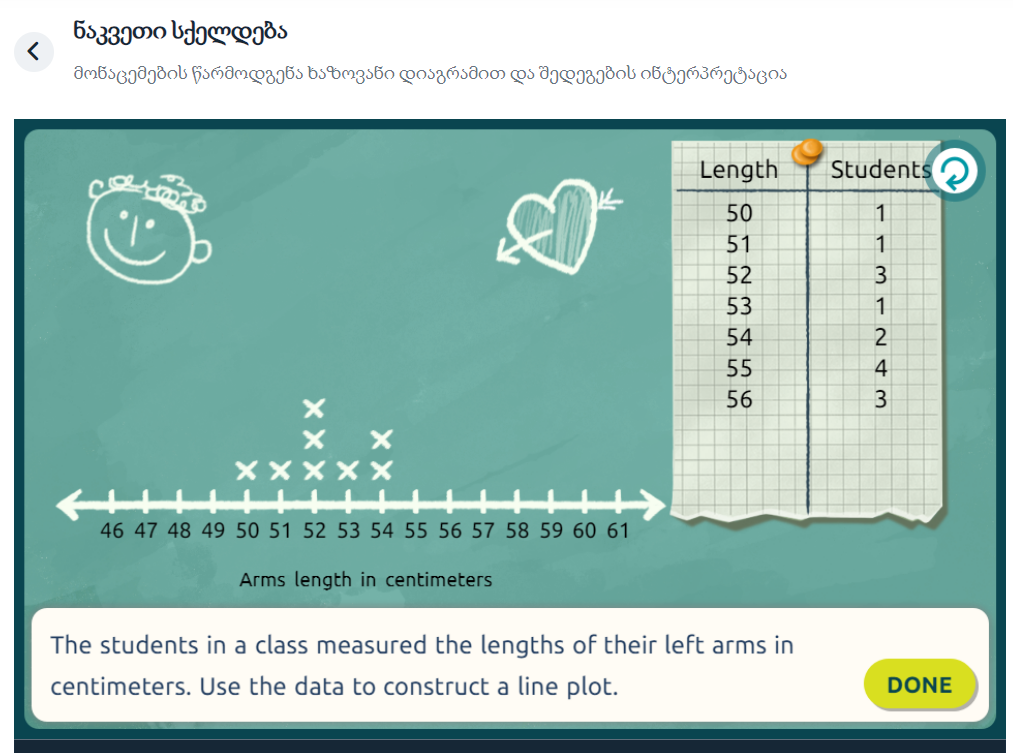
წინარე ცოდნის გააქტიურებლად, სასწავლო პლათფორმის matific.com -ზე მათემატიკური აქტივობები/თამაშები გამოვიყენე. მოსწავლეებმა ონლაინ, ინტერაქტიული თამაშების საშუალებით გაიხსენეს ცნებები. მონაცემთა წარმოდგენის ხერხები. დიაგრამა. პიქტოგრამა.
მოსწავლეები პასუხობენ ფაქტობრივ (რა?) და კონცეპტუალურ შეკითხვებს (როგორ? რატომ?)
- მონაცემთა შეგროვების რომელ ხერხებს იცნობ?
- რას ნიშნავს შევაგროვოთ მონაცემები?
- როგორ ვარჩევთ მონაცემთა შეგროვების მეთოდს?
- როგორ გამოიყენებ მიღებულ მონაცემებს?
- როგორ შეიძლება წარმოვადგინოთ მონაცემები თვალსაჩინო ფორმით? აღწერე თითოეული მათგანი
- რა არის სვეტოვანი დიაგრამა?
- რა არის პიქტოგრამა?
- კიდევ რა ხერხით შეიძლება მონაცემების წარმოდგენა?
- რამდენად ეფექტურია დიაგრამები ამოცანაში მოცემული პირობის წარმოსაჩენად და როგორ გვეხმარება ის მონაცემების გააზრებაში?
გთავაზობთ სასწავლო აქტივობების ბმულებს, რაც დაეხმარათ მოსწავლეებს ხალისით აღედგინათ მონაცემებთან დაკავშირებული უკვე ნასწავლი ცნებები და პროცედურები
https://www.matific.com/ar/en-us/home/maths/episode/FishTankGraphingScaledBarGraphUpTo50/?grade=grade-4
https://www.matific.com/ar/en-us/home/maths/episode/LinePlotFromTableMetricUnits/?grade=grade-5
აქტივობა 2. ძირითადი ცნებები:
მოსწავლეებს ვაცნობ ძირითად ცნებებს რამდენიმე რეალური მაგალითის მოყვანით და განმარტავ (ზოგჯერ თავადაც აღმოაჩენენ) მათი პოვნის პროცესს მოცემულ მონაცემებში.
| ცნება | მაგალითი | ფორმულა. | ||||||||||||||||||||||||||
| საშუალო
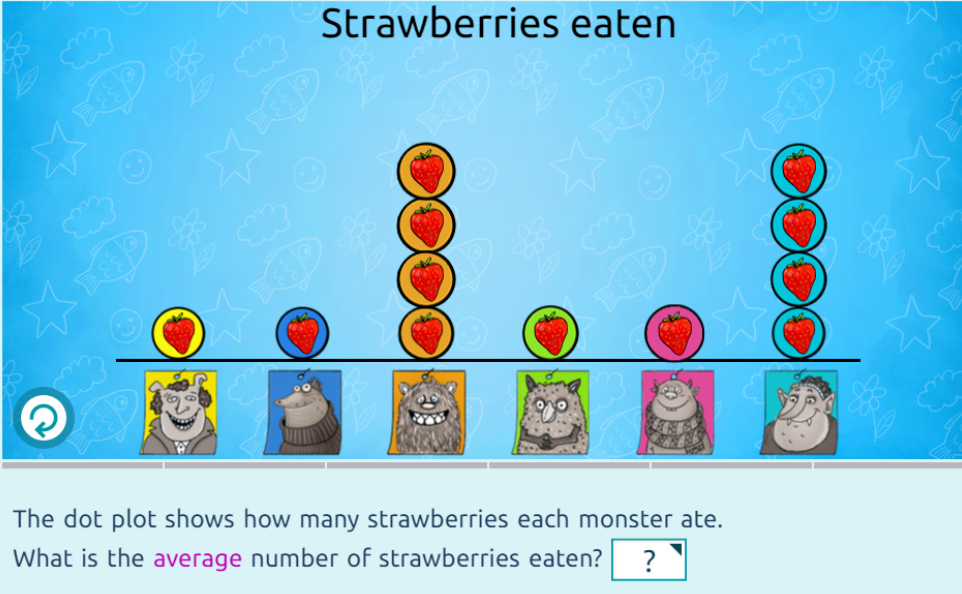
არითმეტიკული საშუალოს ცნების გასააზრებლად ყურადღებას ვამახვილებინებ ისეთ ცხოვრებისეულ მაგალითებზე სადაც ჩნდება საშუალოს პოვნის აუცილებლობა.
|
ჩვენ ვიყენებთ საშუალოს რამდენიმე რეალურ სიტუაციებში გაუცნობიერებლად.
ჯანსაღი ადამიანებისთვის, საშუალო დღიური წყალი მამაკაცებისთვის არის დაახლოებით 15,5 ჭიქა, ხოლო ქალებისთვის დაახლოებით 11,5 ჭიქა. ფაქტობრივად, ყველას არ სჭირდება ერთი და იგივე რაოდენობით წყალი. ზოგმა შეიძლება დალიოს 15,5/11,5 ჭიქაზე ნაკლები, ხოლო ზოგმა შეიძლება დალიოს 15,5/11,5 ჭიქაზე მეტი. ეს ის სიტუაციაა, როდესაც ჩვენ ვიყენებთ საშუალო არითმეტიკის კონცეფციას.
|
ამ ტიპის რეალური ცხოვრების მაგალითების ახსნის შემდეგ მასწავლეებს წარვუდგენ საშუალოს ფორმულას
განვიხილოთ სიტუაციური მაგალითი: 1) მათემატიკის თემების შემაჯამებელი შეფასებები გიორგისათვის ასეთია: 7, 10, 6, 5, 6, 5, 6, 6 მაშინ საშუალო ქულა გიორგის შეფასებისა იქნება
2) ვიპოვოთ კლასის საშუალო ქულა გამოცდაზე, იგივე პრინციპით: მოსწავლეთა შეფასებაა: 8, 10, 7, 10, 5, 9, 7, 5, 6, 8, 9, 10, 7, 10, 5, 9, 7, 9, 10, 7, 10, 9, 7, 10, 7. მოსწავლეები მსჯელობენ რას გვეუბნება საშუალო და ყოველთვის იქნება თუ არა საშუალო არითმეტიკული კლასის საგამოცდო შედეგების საშუალო მაჩვენებელი?(როგორი მონაცემები იწვევს ასეთ შედეგს?) შეუძლია თუ არა თითოეულ მოსწავლეს შეადაროს საკუთარი ნიშანი კლასის საშუალოს. რა სარგებელს მისცემს ეს მოსწავლეს?(შეამოწმოს თავისი მიღწევები კლასში და გადაწყვიტოს, უნდა გააუმჯობესოს თუ არა შედეგი?)
|
||||||||||||||||||||||||||
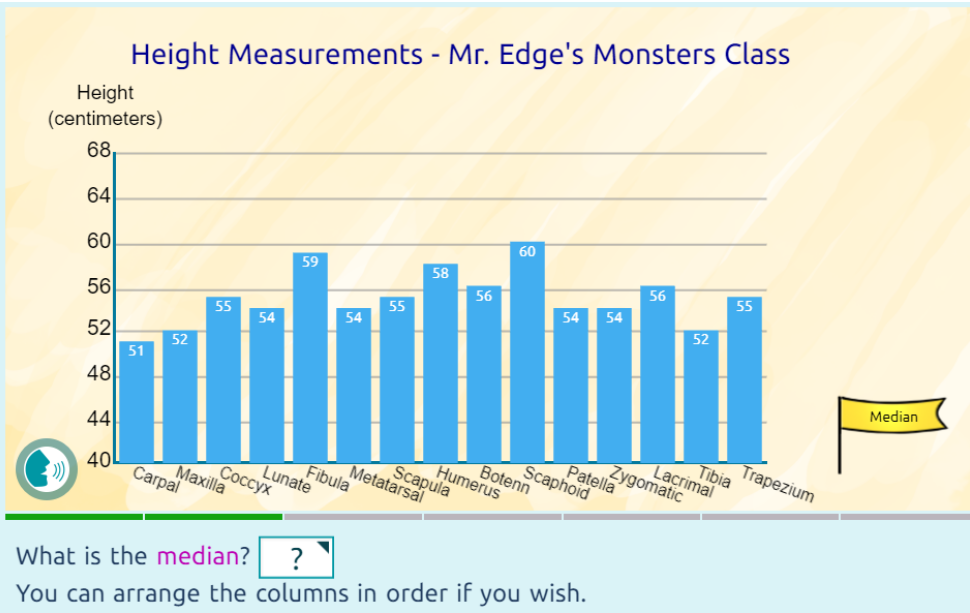
| მედიანა
მოსწავლეებს ვაცნობ მედიანას ცნებას რეალური ცხოვრებისეული მაგალითების მოყვანით. |
დავუშვათ, ჩვენი სკოლის დირექტორი გეგმავს ჩვენი სკოლის მე-6 კლასის ყველა მოსწავლეს მიაწოდოს შეკერილი სასკოლო ფორმა, მაგრამ მას დრო არა აქვს ყველა გოგონა /(ვაჟი) გაზომოს. ის ფიქრობს, რომ მკერავს უნიკალური ზომა მიაწოდოს. საკითხავია, რომელი ზომა უნდა მიიღოს მან, როგორც იდეალური მთელი კლასისთვის? მოსწავლეები ჩაერთნენ დისკუსიაში. თავად მივიდნენ დასკვნემდე, რომ
ცხადია, ესაა „შუა“ ზომა. იმიტომ, რომ თუ ყველაზე დაბალი მოსწავლის ზომებს იდეალურად ავიღებთ, კაბა ყველაზე მაღალი მოსწავლისათვის იქნება ზედმეტად ვიწრო და თუ ყველაზე მაღალი მოსწავლის ზომებს იდეალურად ავიღებთ, კაბა იქნება ზედმეტად თავისუფალი(დიდი) ასე რომ, იდეალური იქნება, თუ ავიღებთ საშუალო მოსწავლის ზომებს. ამ გზით შემომაქვს მედიანის ცნება |
მედიანა არის მონაცემთა ერთობლიობის შუა წერტილი—მონაცემთა ნახევარი ნაკლებია მედიანაზე და ნახევარი მეტია.
ვიპოვოთ მედიანა, ნიშნავს:
|
||||||||||||||||||||||||||
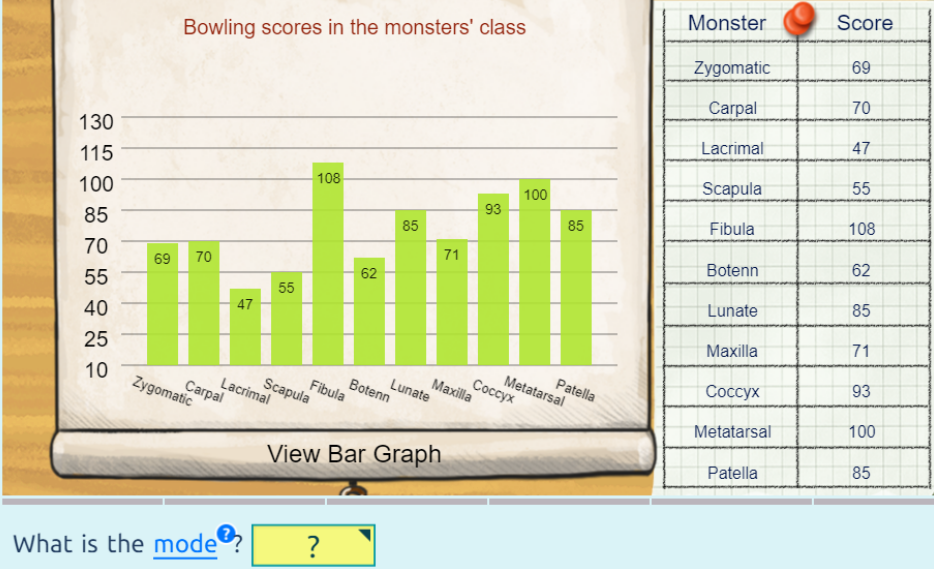
| მოდა | მოსწავლეებს ვაცნობ მოდის ცნებას აქტივობის ჩატარებით, „კლასის ლიდერის არჩევა“
30 მოსწავლიან კლასში ლიდერის კანდიდატურად 5 მონაწილეა დასახელებული. მოსწავლეები თავად მონაწილეობენ თავიანთი კლასის ლიდერის არჩევაში არჩევნების ჩატარების შემდეგ კონკურსანტმა A მიიღო 8 ხმა, კონკურსანტმა B მიიღო 12 ხმა. კონკურსანტმა C მიიღო 3 ხმა, კონკურსანტმა D მიიღო 5 ხმა. კონკურსანტმა E მიიღო 2 ხმა. მოსწავლეებს ვეკითხები, -ვინ არის გამარჯვებული?. პასუხი აშკარად არის “B”, რადგან ის უფრო პოპულარულია სხვებს შორის. მშსდმ მოდა სხვა არაფერია, თუ არა მონაცემთა ყველაზე პოპულარული ან ყველაზე ხშირი მნიშვნელობა. |
მოდა არის მონაცემებში ყველაზე ხშირი მნიშვნელობა. და შემდგომ განმარტავ, რომ ზოგიერთ მონაცემს შეიძლება ჰქონდეს ერთი ან 1-ზე მეტი მოდა ან არ ჰქონდეს.
მოსწავლეებს ვთავაზობ რამდენიმე მაგალითს იმის დასადგენად, რომ ყველა მოსწავლეს ესმის რა არის მოდა და როგორ უნდა მოძებნოს იგი
|
||||||||||||||||||||||||||
აქტივობა 3. სავარჯიშოები:
| მოსწავლეებს ცნებების უკეთ გაგება გაზრებისათვის ვთავაზობ matific.com -ის პლათფორმის ელექტრონულ აქტივობებს, რომლის მიზანია მოდის, მედიანისა და საშუალოს კონცეპრუალური გაგება. ძირითადად ექვს შეკითხვიანი სახალისო ტესტია, რომლისთვისაც მოსწავლეს დასჭირდება 4-5 წთ. მცდარი პასუხის შემთხვევაში პროგრამა გაძლევს მისი გამოსწორების უფლებას, რაც ერთგვარად მოსწავლის განმავითარებელ შეფასებად ითვლება. (აქვე მინდა აღვნიშნო, ჩემი სკოლა ჩართულია ბილინგვური განათლების პროგრამაში დაწყებით საფეხურზე. მოსწავლეები იყენებენ Max მათემატიკის სახელმძღვამელოებს და მათთვის უცხო არაა ინგლისურ ენაზე მათემატიკური ტერმინები, გარდა ამისა მოსწავლეებს შეუძლიათ translate- ის გამოყენებაც)
https://www.matific.com/ar/en-us/home/maths/episode/MedianUsingHistogramLargeNumbers/
https://www.matific.com/ar/en-us/home/maths/episode/VariabilityUsingHistogramAndBoxPlotVariability/?grade=grade-6 https://www.matific.com/ar/en-us/home/maths/episode/MeanWithFruitOnes/?grade=grade-6
|
|
აქტივობა 4. სავარჯიშოები ინდივიდუალური მუშაობისათვის, ამოწმებს რამდენად გაიაზრეს ცნებები. (თითოეული მოსწავლისათვის ერთი ბარათი)
| ბარათი# | მონაცემების მიხედვით იპოვე შემდეგი რიცხვითი მახასიათებლები | |||||||
| 1 |
|
|||||||
| 2 |
|
|||||||
| 3 |
|
|||||||
| 4 |
|
|||||||
| 5 |
|
|||||||
| 6 | . . . |
აქტივობა 5. ცენტრალური ტენდენციის საზომები ზოგჯერს არასაკმარისა მონაცემთა დასახასიათებლად?
მოსწავლეებს ეძლევათ კონტექსტური ამოცანა, სადაც უნდა გამოიყენონ ცენტრალური ტენდენციის საზომები კონკრეტული სიტუაციის მიხედვით, იმსჯელონ და მიიღონ გადაწყვეტილება
| სიტუაციური ამოცანა:
გიორგი სოფელში გაემგზავრა. აღმოჩნდა რომ სოფლის მდინარეზე გადასასვლელი ხიდი დაზიანებულია. ამიტომ მეორე ნაპირზე გადასასვლელად მას შემოვლითი გზით 10 კმ-ის გავლა ესაჭიროება. გიორგიმ მოიძია ინფორმაცია მდინარის შესახებ და ცნობარში ამოიკითხა რომ მდინარის წყლის დონის საშუალო სიღრმე არის 0,7 მ-ია. ამავდროულად 80% -ისათვის სიღრმე 0,3 მ-ია, ხოლო 20% -სთვის 2,3მ. გიორგიმ ცურვა არ იცის. ის ფიქრობს რომ 70 სმ სიმაღლის წყალს თავისუფლად გადაკვეთს, მით უფრო რომ მდინარე მდორედ მოედინება. რას ურჩევდით გიორგის, ამ მონაცემზე დაყრდნობით გარისკოს მდინარის გადალახვა? დასკუსია: -მდინარის სიღრმე ყოველთვის 0,7 მ-ია? -მდინარის სიღრმე ზოგიერთ ადგილში არის თუ არა 0,7 მ-ზე ბევრად დიდი, ან ნაკლები? დაასახელეთ ეს ზომები ამოცანის პირობიდან. -გადაამოწმეთ ზემოთაღწერილი სუტუაციის მიხედვით, მოცემული მონაცემების საშუალო ნამდვილად არის თუ არა 0,7მ? -რა არის ამ მონაცემებისთვის მოდა? მედიანა? -საკმარისია თუ არა მხოლოდ იმის ცოდნა რომ მდინარის საშუალო სიღრმე არის 0,7მ, მოდა 0,3მ და მედიანა 0,3მ? რას ურჩევთ გიორგის გადაკვეთოს მდინარე თუ შემოვლით 10 კმ -იანი გზის გავლით მივიდეს შინ?
|
დისკუსიის შემდეგ გამოაქვთ დასკვნა რომ, ცენტრალური ტენდენციის ზომები არ იძლევა საერთო სურათს და შეიძლება იყოს შეცდომაში შემყვანი.
ცენტრალური ტენდენციის საზომები ზოგჯერს არასაკმარისია მონაცემთა დასახასიათებლად. ცენტრალურ ტენდენციაზე დიდ გავლენას ახდენს სხვა ფაქტორები, რომელთა შესახებ ცოდნას მომდევნო წლებში გავაფართოვებთ.
გამოყენებული ლიტერატურა
- ეროვნული სასწავლო გეგმა https://mes.gov.ge/content.php?id=3929&lang=geo
- დაწყებითი საფეხურის დეტალური განაწილება მასწავლებლებისთვის, ინდიკატორებით https://math.ge/kurikulumi/
- მათემატიკის გზამკვლები მე-6 კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/meegvse-klasi/
- https://www.expii.com/t/word-problems-when-to-use-mean-median-and-mode-4645
- https://www.matific.com/gb/en-gb/home/