რატომ უნდა ვიცოდეთ ფიზიკა

(პირველი ნაწილი)

ადამიანს მთელი სიცოცხლის განმავლობაში უხდება ბუნებრივ მოვლენებზე დაკვირვება, მათი მახასიათებელი სიდიდეების გაზომვა, შესწავლა და გაანალიზება. ადამიანს უნდა შეეძლოს დაკვირვებისა და გაზომვის შედეგების პრაქტიკულ საქმიანობაში გამოყენება.

გავზომოთ რაიმე სიდიდე, ნიშნავს შევადაროთ ის წინასწარ ანალოგიური ზომის ერთეულად შერჩეულ ან ეტალონურ სიდიდეს.

გაზომვა ორი სახისაა: პირდაპირი და არაპირდაპირი.

გაზომვა პირდაპირია, თუ მზომი ხელსაწყოთი უშუალოდ იზომება მოვლენის მახასიათებელი სიდიდე.

გაზომვა არაპირდაპირია, როცა სასურველი სიდიდის უშუალოდ გაზომვა შეუძლებელია და მისი გამოთვლა ხდება სხვა პირდაპირი გზით გაზომილი სიდიდეების დახმარებით.

არაპირდაპირი მეტრული გაზომვის რამდენიმე მეთოდი არსებობს. გაზომვა შეიძლება ვაწარმოოთ როგორც მათემატიკურ დასკვნებზე დაყრდნობით, ისე ფიზიკის კანონების მოშველიებითაც. განვიხილოთ მაგალითები.

ამოცანა 1. გამოვთვალოთ სფერული სეგმენტის რადიუსი (ნახ. 1) (AB სეგმენტი გამოყოფილია მუქი ფერით)

1. გავავლოთ DC დიაგონალი, A წერტილი შევაერთოთ D და C წერტილებთან. მაშინ      DAC=90⁰ როგორც დიამეტრზე დაყრდნობილი კუთხე. ამრიგად,   DAC მართკუთხაა.წარმოვიდგინოთ, რომ შევავსეთ სეგმენტი სფერომდე (წყვეტილი წირეები ნახატზე). აქვე ნახატზე გამოკვეთილია წარმოსახვითი სფეროს AB ქორდაზე გამავალი დიამეტრული კვეთა – ACBD წრეწირი.

ვისარგებლოთ თეორემით:

თუ მართკუთხა სამკუთხედში მართი კუთხის წვეროდან ჰიპოტენუზაზე დაშვებულია მართობი, მაშინ:

1. დაშვებული მართობის სიგრძე საშუალო პროპორციულია ჰიპოტენუზის მონაკვეთებისა.
2. თითოეული კათეტი საშუალო პროპორციულია ჰიპოტენუზისა და ჰიპოტენუზაზე ამ კათეტის გეგმილისა.

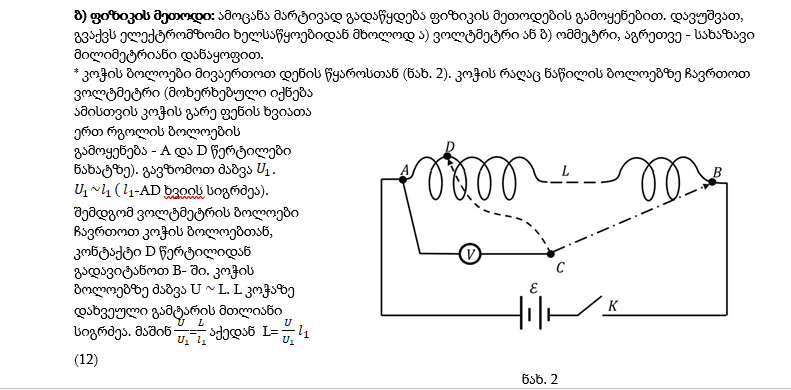
ამოცანა  2 . განსაზღვრეთ  კოჭზე  დახვეული  გამტარის  სიგრძე

ა) მათემატიკური მეთოდით ეს ამოცანა ასე შეიძლება გადაიჭრას: ვიპოვოთ ერთი ხვიის სიგრძე. ამისთვის სახაზავის, საზომი ლენტის ან ძაფის გამოყენებით გავზომოთ ხვიის დიამეტრი – D. ხვიას სიგრძე იქნება  = D. შემდგომ დავთვალოთ კოჭში ხვიათა რაოდენობა – N და L=N  (11)- ით გამოვიანგარიშოთ კოჭში ხვიის სიგრძეს.

თუ ხვიები ისეა კოჭზე, რომ გვაქვს ხვიათა საკმაოდ ბევრი ფენა, მაშინ ასეთი ოპერაცია უნდა შესრულდეს თითოეული ფენისათვის და მიღებული შედეგები შეჯამდეს, რაც საკმაოდ შრომატევადია, ძნელია და ზოგჯერ პრაქტიკულად შეუძლებელიც.

ორივე ხერხი მათემატიკურ მეთოდზე მარტივია, მაგრამ არცთუ მნიშვნელოვნად.

აღსანიშნავია, რომ ამ ორიდან რომელიმე მეთოდის გამოყენებისას არ არის საჭირო კოჭის ხვიების ცალ-ცალკე დათვლა, ამიტომ ამოცანაში დასმული პრობლემის გადასაჭრელად ფიზიკის ხერხით სარგებლობა უფრო მარტივია, ვიდრე მათემატიკური მეთოდით.

გ) არსებობს კოჭზე დახვეული გამტარის სიგრძის გამოთვლის უფრო მარტივი გზა, იმ შემთხვევაშიც კი, თუ სიგრძის გაზომვის არავითარი საშუალება არ გაგვაჩნია.

ავიღოთ წვრილი ძაფი, შემოვახვიოთ ის კოჭის გარე ფენის ერთ ხვიაზე, შემდეგ ძაფზე ვერტიკალურად ჩამოვკიდოთ მცირე ზომის ბურთულა. ამ გზით მიღებული ქანქარა მოვიყვანოთ რხევით მოძრაობაში. მაშინ ამოცანა N1-ში დიამეტრის (რადიუსის) გამოთვლის ფიზიკის მეთოდებში აღწერილი ხერხით ვიპოვით ძაფის, იმავე კოჭის ერთი ხვიას სიგრძეს . შემდგომ (12), (13) ფორმულებით ადვილად ვიპოვით კოჭზე დახვეული გამტარის მთლიან სიგრძეს.

* აღსანიშნავია, რომ ეს უკანასკნელი ხერხი გამოდგება იმ შემთხვევისთვისაც, როცა კოჭის ხვიები დამზადებულია არაგამტარი ნივთიერებისაგან. ამ შემთხვევაში უნდა განისაზღვროს კოჭის ვერტიკალურ კვეთაში არსებული (სასურველია ერთი ხვიების წყობა) ხვიების მთლიანი სიგრძე. თუ ეს შესაძლებელია სახაზავით, მაშინ გარე ფენაზე ხვიების დათვლით მარტივად ვიპოვოთ ხვიათა მთლიან სიგრძეს.

თუ არ გვაქვს სიგრძის გაზომვის საშუალება, საჭიროა განისაზღვროს ძაფის საშუალებით ერთი ვერტიკალური ფენის სიგრძე. ასეთი ძაფის ერთი ბოლო ჩამოვკიდოთ ვერტიკალურად, მეორეზე მივაბათ მცირე ზომის ბურთულა. ასეთი ქანქარა მოვიყანოთ რხევით მოძრაობაში და უკვე განხილული ხერხით ვიპოვოთ ძაფის სიგრძე, კოჭის ერთ ვერტიკალურ კვეთაში არსებული ხვიის სიგრძე-l. შემდგომ დავთვალოთ ზედა ფენაში ხვიების რაოდენობა – N და ფორმულით L=Nl ვიანგარიშოთ მთლიანი ხვიების სიგრძე. ცხადია, აღწერილი ფიზიკური მეთოდები მათემატიკურზე გაცილებით მარტივია.

გამოყენებული ლიტერატურა:

1. ფიზიკა. 7, 8, 9, 10, 11 კლ. სახელმძღვანელო. გ. გედენიძე, ე. ლაზარაშვილი
2. ფიზიკა. 7, 8, 9, 10, 11 კლ. სახელმძღვანელო. ე. ტატიშვილი
3. В. Н. Ланге, Сборник вопросов и задач по физике на смекалку, 1978
4. ზ. ბართაია, „აზროვნების განვითარების ეტაპები ფიზიკის გაკვეთილზე ბლუმის ტაქსონომიის შესაბამისად (ერთი ამოცანის მაგალითზე)“
5. მათემატიკა. 7, 8, 9, 10, 11 კლ. სახელმძღვანელო. გ. გოგიშვილი, გ. თევზაძე, ი. მებონია, ე. ქურჩიშვილი
6. ზურაბ ბართაია, „ბიჰევიორიზმის კონცეფცია და მისი გამოყენება სწავლებაში“