მათემატიკური წიგნიერება მოითხოვს არა მხოლოდ ალგებრული წესების ცოდნას, არამედ ამ ცოდნის ინტეგრირებას რეალური სამყაროს რთული მოვლენების ასახსნელად. წინა სტატიაში „სინუსოიდური ფუნქციების კვლევითი ანალიზი და სიღრმისეული გაგება“ დეტალურად განვიხილეთ, როგორ იქნა მიღწეული ფუნქციის თითოეული პარამეტრის (A, B, C, D) სიღრმისეული გაგება ცალკეული კვლევითი აქტივობების საშუალებით.
ამ სტატიაში ყურადღებას ვამახვილებ გაკვეთილის მთავარ, გადამწყვეტ ეტაპზე – ცალკეული ცოდნის ფუნქციურ ინტეგრირებაზე. მოსწავლეებმა შეძლეს ოთხივე პარამეტრის ერთდროულად გამოყენება რეალური პერიოდული მოვლენის (ზღვის მოქცევა) მოდელირებისთვის. სტატია აღწერს ამ კომპლექსური შემაჯამებელი დავალების ეტაპებს, მოსწავლეთა მიერ მიღწეულ შედეგებს და ადასტურებს, რომ დროის ინვესტიციამ ფორმულების მექანიკური დამახსოვრება ჩაანაცვლა პროგნოზირებისა და ლოგიკური ანალიზის უნარით.
კლასი: მე-11
მიმართულება: ალგებრა და კანონზომიერება
თემატური ბლოკი: შესაბამისობა, გრაფიკი, დამოკიდებულება, ფუნქცია
| სამიზნე ცნებები | ||
| 1. მათემატიკური მოდელი | 2. კანონზომიერება | 3. ლოგიკა |
| რეალური პერიოდული მოვლენების (ტალღა, ტემპერატურა) აღსაწერად y(t) = A sin(B(t-C)) + D ფორმულის საშუალებით რეალური სიტუაციის მოდელირება და მომავალი მდგომარეობის გამოთვლა. | პერიოდული მოვლენების და მათი აღმწერი ფუნქციების გრაფიკების განხილვა. პარამეტრების (A, B, C, D) კვლევა/ანალიზი. | ფუნქციური დამოკიდებულებებისა და ტრიგონომეტრიული იგივეობების ანალიზი. მსჯელობა: ლოგიკური დასკვნების გამოტანა. (მიზეზ-შედეგობრივი კავშირი პარამეტრებსა და გრაფიკს შორის). |
მათემატიკის სტანდარტის შედეგები:
მათ.საშ.3.: შესასწავლი მოვლენიდან გამომდინარე ცვლად თუ მუდმივ სიდიდეთა შორის შესაბამისობის, ფუნქციური კავშირის დამყარება და წარმოდგენა შესაბამისი ერთი ან რამდენიმე ფორმით; ფუნქციის გამოყენება სხვადასხვა კონტექსტში ცვლილებათა გასაანალიზებლად და რეალური მოვლენების მოდელირებისთვის.
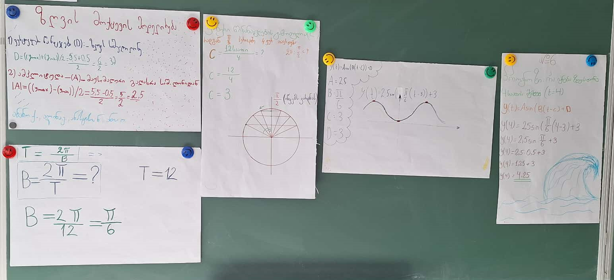
შემაჯამებელი დავალება, სადაც მოსწავლეებმა გამოიყენეს ოთხივე პარამეტრი ერთდროულად, ზღვის მოქცევის მოდელის შესაქმნელად.
მოსწავლეებმა შეძლეს, დავალების შესრულება და პრეზენტაცია. აქვე გთავაზობთ მოსწავლეთა ნამუშევრების ფოტოს და შეფასების რუბრიკას
| დონე | ცნება: მათემატიკური მოდელი | ცნება: კანონზომიერება | ცნება: ლოგიკა და მსჯელობა |
| მაღალი/ სიღრმისეული | მოსწავლე ზუსტად განსაზღვრავს ოთხივე პარამეტრს (A, B, C, D) და ქმნის სრულყოფილ ფუნქციურ მოდელს. ზუსტად იყენებს მოდელს მომავალი მდგომარეობის პროგნოზირებისთვის (t=4 საათი). | სრულად ესმის ოთხივე პარამეტრის დამოუკიდებელი გავლენა გრაფიკზე და განასხვავებს ვერტიკალურ სტრუქტურას (A, D) ჰორიზონტალური სტრუქტურისგან (B, C). | მსჯელობა არის სრულყოფილი: ამტკიცებს, თუ რატომ არის საჭირო C=3 საათით წანაცვლება (ტალღის დაცემის დასაწყისი t=0-ზე) და ლოგიკურად განმარტავს D-ს, როგორც წონასწორობის ცენტრს. |
| კარგი/
ამომწურავი |
მოსწავლე განსაზღვრავს ოთხივე პარამეტრს, უშვებს მცირე მექანიკურ შეცდომებს (B, C, D ან A-ს გამოთვლისას). ქმნის ფუნქციურ მოდელს და ახორციელებს სწორ პროგნოზს (t=4 საათი), თუმცა მცირედი უზუსტობით. | ესმის და განმარტავს პარამეტრების უმეტესობის გავლენას. პერიოდის (B) და ამპლიტუდის (A) კავშირი მოდელთან მკაფიოდ აქვს გადმოცემული. | მსჯელობა არის სწორი: ფაზური წანაცვლების (C) ლოგიკა (T/4) სწორად არის გამოყენებული, მაგრამ განმარტება ნაკლებად დეტალურია. |
| საშუალო/
ნაწილობრივი |
მოსწავლე სწორად განსაზღვრავს მხოლოდ ვერტიკალურ პარამეტრებს (A, D) ან მხოლოდ A, B-ს. C პარამეტრის განსაზღვრისას უშვებს არსებით შეცდომას (ვერ ითვალისწინებს T/4 წანაცვლებას). | ნაწილობრივ ესმის კანონზომიერებები: ამოიცნობს A და D პარამეტრებს, მაგრამ უჭირს B და C კომპონენტების გავლენის ინტეგრირება ერთ მთლიანობაში. | მსჯელობა არის ზედაპირული: აღწერს ნაბიჯებს, მაგრამ ვერ ხსნის ლოგიკურ კავშირს t=0 პირობასა და ფაზურ წანაცვლებას შორის. |
| დაბალი/
ელემენტარული |
მოსწავლე ცდილობს მოდელის შექმნას, მაგრამ არასწორად განსაზღვრავს პარამეტრების უმრავლესობას. მოდელი არაფუნქციურია. | მხოლოდ ელემენტარული ცნებების (მაგ., მაქსიმუმი/მინიმუმ) ამოცნობა შეუძლია. პერიოდისა და ფაზის კანონზომიერებების გააზრება უჭირს. | მსჯელობა არის არასწორი ან არარსებული. ვერ ხსნის ვერტიკალური ან ჰორიზონტალური წანაცვლების მიზეზებს. |
ამ კომპლექსურმა დავალებამ, სადაც მოსწავლეებს მოუწიათ ლოგიკის, კანონზომიერებისა და მათემატიკური მოდელირების ცნებების ერთდროულად გამოყენება, წარმოაჩინა მოსწავლეთა მაღალი კომპეტენცია – მათ არა მხოლოდ შეძლეს პარამეტრების A, B, C, D, ინტეგრირება და ზღვის მოქცევის რთული მოდელის შექმნა, არამედ აანალიზებდნენ, თუ რატომ უნდა იყოს ტალღა წანაცვლებული მარჯვნივ და რატომ წარმოადგენს D პარამეტრი წონასწორობის ცენტრს. ეს იყო მათემატიკის გამოყენება პროგნოზირების მიზნით, რაც უმნიშვნელოვანესია ფუნქციების შესწავლისას.
შედეგები ცხადყოფს: სინუსოიდური ფუნქციების შესწავლა უნდა მიდიოდეს აბსტრაქციის მიღმა. მხოლოდ კონტექსტის შესაბამისი, სიღრმისეული კვლევა აქცევს მოსწავლეებს ფორმულების შემსრულებლებიდან მათემატიკური მოდელების შემქმნელებად, რაც მათ საშუალებას აძლევს, გააანალიზონ და გააკონტროლონ პერიოდული პროცესები რეალურ სამყაროში.
გამოყენებული ლიტერატურა:
- ეროვნული სასწავლო გეგმა https://mes.gov.ge/content.php?id=3929&lang=geo;
- მათემატიკის გზამკვლევი მე-11 კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/metertmete/;
- https://courses.lumenlearning.com/suny-osalgebratrig/chapter/graphs-of-the-sine-and-cosine-functions/