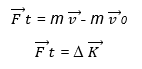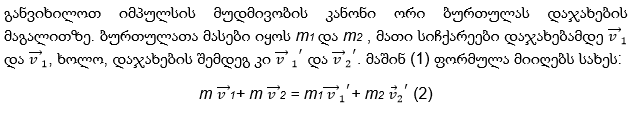ჩვენს სწრაფად განვითარებად ეპოქაში ხელოვნური ინტელექტი თანდათან იკავებს ცხოვრების სხვადასხვა სფეროს. მონაცემთა მოდელირება, სიმულაციები და ვირტუალური გარემო ჩქარი ტემპით იმკვიდრებს ადგილს განათლებასა და სამეცნიერო სივრცეში. ასეთ პირობებში რეალური ექსპერიმენტების მნიშვნელობა კიდევ უფრო თვალსაჩინო და ფასეული ხდება. ციფრული ტექნოლოგიები უდიდეს შესაძლებლობებს იძლევა, თუმცა ისინი ხშირად ეფუძნება წინასწარ არსებულ მონაცემებსა და თეორიებს. რეალური ექსპერიმენტი კი გვინარჩუნებს ფიზიკურ კავშირს სამყაროსთან – ის არა მხოლოდ ამყარებს და ამდიდრებს თეორიულ ცოდნას, არამედ აჩენს კითხვებს, როგორიც ციფრულ მოდელებში შესაძლოა საერთოდაც არ გამოიკვეთოს. რეალური ექსპერიმენტი მოზარდს უვითარებს პრაქტიკულ უნარ-ჩვევებს, შეცდომებით სწავლას, ხელს უწყობს კრიტიკულ და მეცნიერულ აზროვნებას. ექსპერიმენტი არ არის მხოლოდ შედეგის მიღება – ეს არის აღმოჩენის პროცესი, როდესაც მოზარდი დაკვირვებით და გამოცდილებაზე დაყრდნობით იღებს ჭეშმარიტ ცოდნას. სწორედ ასეთ პროცესში ვითარდება ადამიანური სოციო-ემოციური უნარები, რაც სრულად ვერასოდეს ჩანაცვლდება ალგორითმით.
წინამდებარე სტატიაში წარმოგიდგენთ ექსპერიმენტს იმპულსის მუდმივობის კანონის შესასწავლად. მისი მთავარი უპირატესობა არის სკოლის პირობებში მისი ჩატარების სიმარტივე და ხელმისაწვდომობა. ძაფზე დაკიდებული ბურთულების ურთიერთქმედებაზე დაკვირვებით შესაძლებელია დრეკად და არადრეკად დაჯახებებთან დაკავშირებული კანონზომიერებების შესახებ ცოდნის გაღრმავება. ენერგიების გამოთვლის საშუალებით კი შეგვიძლია უფრო ზუსტად დავადგინოთ, კონკრეტულ შემთხვევაში რა ტიპის დაჯახებასთან გვაქვს საქმე.
სანამ დაკვირვებისა და ექსპერიმენტის მსვლელობის განხილვაზე გადავალთ, გავიხსენოთ იმპულსის რაობა და მასთან დაკავშირებული ძირითადი თეორიული ცნებები.
ნიუტონის კანონების საშუალებით შესაძლებელია მექანიკის ძირითადი ამოცანის გადაწყვეტა. თუ გვეცოდინება სხეულზე მოქმედი ძალა (ძალების ტოლქმედი) და სხეულის მასა, შევძლებთ განვსაზღვროთ აჩქარება, რომლის საშუალებითაც ვიპოვით სხეულის სიჩქარეს, გადაადგილებასა და ბოლოს კოორდინატს.
არსებობს შემთხვევები, როდესაც სირთულეს წარმოადგენს სხეულზე მოქმედი ძალების განსაზღვრა. მაგალითად, სხეულთა შეჯახების დროს ძალის მოქმედება გრძელდება ძალიან მცირე დროის განმავლობაში. ამასთანავე, სხეულთა შემხები ნაწილაკების დეფორმაცია რთული სახისაა. მსგავს შემთხვევებში ძნელია აჩქარების განსაზღვრა. ამ დროს უმჯობესია, გამოვიყენოთ ისეთი სიდიდე, რომელიც სისტემას დაახასიათებს შეჯახებამდე და შეჯახების შემდეგ. ასეთი სიდიდეა იმპულსი, რაც ლათინურად „ბიძგს“, „დარტყმას“ ნიშნავს. იმპულსის საშუალებით სხეულთა შეჯახებისას ურთიერთქმედების შედეგი (ეფექტი) განისაზღვრება არა მხოლოდ მიღებული სიჩქარით, არამედ სხეულის მასით.
იმპულსის ცნების შემოტანა უკავშირდება ფრანგ მეცნიერს, რენე დეკარტს (1596-1650 წწ). დეკარტმა მას „მოძრაობის რაოდენობა“ უწოდა, რაც ზუსტად განმარტავს ამ ცნების რაობას – სხეულის მოძრაობის „შესაძლებლობას“ ერთდროულად განსაზღვრავს მასა და სიჩქარე. უფრო მოგვიანებით დამკვიდრდა კი ტერმინი „სხეულის იმპულსი“.
იმპულსი განისაზღვრება, როგორც სხეულის მასისა და მისი სიჩქარის ნამრავლი. სხეულის იმპულსი ვექტორული სიდიდეა და მისი მიმართულება ემთხვევა სხეულის სიჩქარის მიმართულებას:
ურთიერთმოქმედ სხეულთა ერთობლიობას სისტემა ეწოდება. სისტემას ეწოდება ჩაკეტილი, თუ მასში შემავალი სხეულები ურთიერთქმედებენ მხოლოდ ერთმანეთზე და არ ურთიერთქმედებენ სხვა სხეულებთან, რომლებიც მოცემულ სისტემაში არ შედიან. სისტემის იმპულსი ეწოდება ამ სისტემაში შემავალი სხეულების იმპულსების ვექტორულ ჯამს:
ჩაკეტილი სისტემისთვის სამართლიანია იმპულსის მუდმივობის კანონი –
ჩაკეტილი სისტემის სხეულთა იმპულსების გეომეტრიული ჯამი არ იცვლება ამ სისტემაში შემავალ სხეულთა შორის ნებისმიერი ურთიერთქმედებისას:
სხეულის იმპულსის ცვლილება განიმარტება, როგორც ძალის იმპულსი. სიდიდეს, რომელიც ძალისა და დროის ნამრავლის ტოლია, ძალის იმპულსი ეწოდება.
ძალის იმპულსი მეტად მნიშვნელოვანი სიდიდეა. იგი ძალის მოქმედების შედეგს ახასიათებს არა მხოლოდ ძალის ზომით, არამედ მისი მოქმედების დროითაც – ძალის მოქმედების შედეგს განსაზღვრავს მისი მოქმედების დრო.
SI- სისტემაში იმპულსის ერთეულია – 1კგ.მ/წმ. ასევე, იმპულსის გასაზომად შეიძლება გამოვიყენოთ ძალის და ამ ძალის მოქმედების დროის ნამრავლი -1 ნ.წმ.
სხეულთა დაჯახებას უწოდებენ აბსოლუტურად დრეკადს, თუ სხეულების თავდაპირველი მექანიკური ენერგია არ გადადის შინაგან ენერგიაში. ასეთი დაჯახების პროცესში წარმოშობილი დეფორმაცია მთლიანად ისპობა. სხეულები აღიდგენენ პირვანდელ ფორმასა და მოცულობას. იმპულსის მუდმივობის კანონი დრეკადი დაჯახებისას გამოისახება მიღებული (2) ფორმულით.
სხეულების შეჯახებისას ყოველთვის წარმოიქმნება ხახუნი, სხეულები დეფორმირდება, წარმოიქმნება ბგერა და ზოგჯერ სინათლეც კი. ეს კი იმას ნიშნავს, რომ მექანიკური ენერგია ნაწილობრივ გარდაიქმნება სხვა სახის ენერგიად. ზოგ შემთხვევაში ასეთი დანაკარგები სიმცირის გამო შეიძლება უგულებელვყოთ (მაგ. ბურთულების დაჯახება).
განვიხილოთ ექსპერიმენტის შინაარსი და მისი განხორციელების ეტაპები.
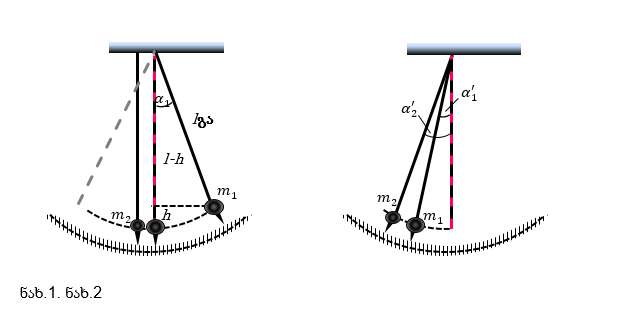
l სიგრძის ძაფებზე ჩამოვკიდოთ m1 და m2 მასის ბურთულები (ნახ.1). ცდის გამარტივების მიზნით, უმჯობესია ერთი ბურთულა (მაგ. m2), წონასწორობაში დავტოვოთ. მაშინ მისი სიჩქარე v2 = 0. აქვე უნდა განიმარტოს აუცილებელი პირობა, რომ m1 ≥ m2, რადგან დაჯახებისას m1 მასის ბურთულამ არ განიცადოს უკუსვლა.
m1 მასის ბურთულა წონასწორობიდან გადავხაროთ დაახლოებით 300 -იანი კუთხით. მისი ნულოვანი დონიდან აწევის სიმაღლე აღვნიშნოთ h-ით. ნახაზის მიხედვით შეიძლება დავწეროთ:
l = h + l cos α1
h = l ( 1- cos α1 )
ექსპერიმენტის ჩასატარებლად წინასწარ უნდა იყოს ცნობილი (ან ავწონოთ) ბურთულათა m1 და m2 მასები. ექსპერიმენტის მსვლელობისას კი უნდა გავზომოთ α1 , α1‘ და α2‘ კუთხეები.
(7), (8) და (9) ფორმულები შევიტანოთ (2) -ე ფორმულაში, მივიღებთ საინტერესო ფორმულას:
m1α1 = m1 α1‘ + m2 α2‘ (10)
აბსოლუტურად არადრეკადი დაჯახების დროს, რა თქმა უნდა, α1‘ = α2‘ .
m1α1 =( m1 + m2) α1‘ (11)
დაჯახების ტიპის დასაზუსტებლად, უნდა შევამოწმოთ ენერგიის მუდმივობის კანონი. ამისათვის, გამოვთვალოთ ენერგიები დაჯახებამდე და დაჯახების შემდეგ და შევადაროთ ერთმანეთს. რაც მეტი გამოვა ენერგიათა სხვაობა, მით უფრო არადრეკადი იქნება დაჯახება.
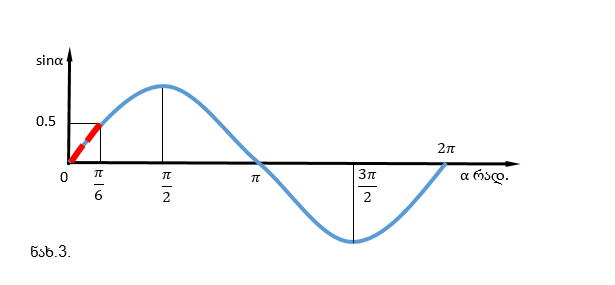
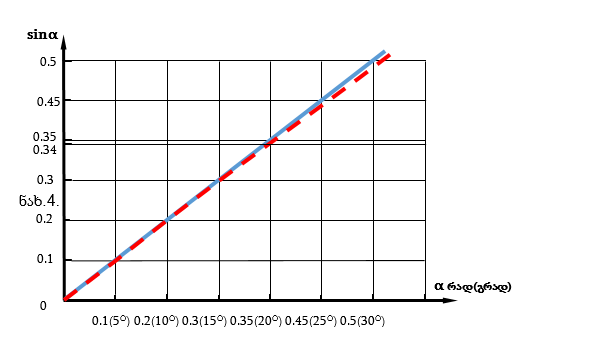
მიღებული ფორმულით, ძაფზე დაკიდებული ბურთულების დაჯახების დროს გადახრის კუთხეებით შესაძლებელია იმპულსის მუდმივობის კანონის შემოწმება. მაგრამ, ამ ფორმულის გამოყენებისას ხაზი უნდა გავუსვათ დაშვებულ წინაპირობას, რომ sin α1 ≈ α1. სინუსი 300– მდე თითქმის წრფივი ფუნქციაა, რადიანებში გაზომილი კუთხე ემთხვევა კუთხის სინუსის მნიშვნელობას. რაც თვალსაჩინოდ ჩანს მოცემულ გრაფიკებზე ( ნახ.3. და ნახ.4).
მე-4 ნახაზზე მკაფიოდ ჩანს sin α-ს α–ზე დამოკიდებულების გრაფიკის (0; 300) უბანი. ამ შუალედში, რადიანებში გაზომილი კუთხის და შესაბამისი სინუსის მნიშვნელობები თითქმის ერთმანეთის ტოლია.
ექსპერიმენტისთვის საჭირო რესურსები:
- შტატივი;
- შტატივზე გვერდიგვერდ ორი ბურთულას თოკი თავისი სამაგრით;
- სახაზავი;
- შტატივის სადგამს მიმაგრებული უნდა ჰქონდეს კუთხის გამზომი;
- სხვადასხვა მასის ორი ლითონის ბურთულა (ცნობილი მასებით);
- ორი პლასტილინის ბურთულა (ცნობილი მასებით).
ექსპერიმენტის მსვლელობა:
- დაკიდეთ შტატივზე დაკიდებულ ძაფებზე ლითონის m1 და m2 მასის ბურთულები;
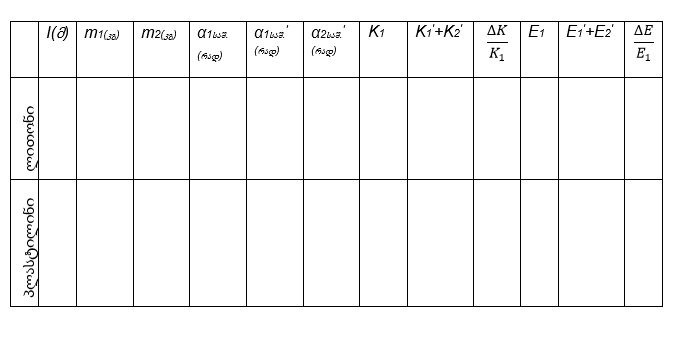
- ბურთულათა მასები შეიტანეთ ცხრილში;
- გაზომეთ ძაფის სიგრძე (I) და მისი მნიშვნელობა შეიტანეთ ცხრილში;
- გადახარეთ m1 მასის ბურთულა დაახლოებით α1 ≤ 300 კუთხით; ცხრილში ჩაინიშნეთ გადახრის კუთხის მნიშვნელობა რადიანებში;
- გაუშვით ხელი m1 მასის ბურთულას;
- წონასწორობაში მყოფი m2 მასის ბურთულასთან შეჯახების შემდეგ, თვალით დააფიქსირეთ ბურთულათა გადახრის შესაბამისი კუთხეები α1‘ და α2‘ – (დააკვირდით და დაიმახსოვრეთ გადახრის α1‘ და α2‘ კუთხეები ვიზუალურად).
- α1‘ და α2‘ კუთხეთა მნიშვნელობები გადაიყვანეთ რადიანებში და შეიტანეთ ცხრილში;
- ცდა გაიმეორეთ სამჯერ და გამოთვალეთ α1, α1‘ და α2‘-ის საშუალო მნიშვნელობები;
- კუთხის საშუალო მნიშვნელობებისთვის გამოთვალეთ იმპულსის K1, K1‘ და K2‘ მნიშვნელობები;
- კუთხის საშუალო მნიშვნელობებისთვის გამოთვალეთ შესაბამისი პოტენციური ენერგიები: E1; E1‘ და E2‘ ;
- შესაბამისი სამუშაო ფორმულების გამოყენებით შეამოწმეთ იმპულსის და ენერგიის შენახვის კანონები;
- მიღებული შედეგები შეიტანეთ ცხრილში;
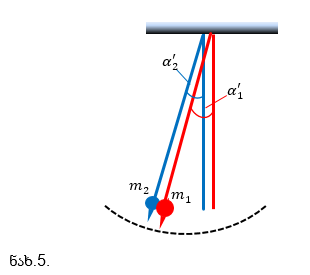
- ექსპერიმენტი გაიმეორეთ პლასტილინის ბურთულებისთვის (ნახ.5.);
- ჩაატარეთ ანალოგიური გამოთვლები და მიღებული შედეგები შეიტანეთ ცხრილში;
- ახსენით ექსპერიმენტის შედეგები.
| ლითონი | N | α1
გრადუსი |
α1
რადიანი |
α1‘
გრადუსი |
α1‘
რადიანი |
α2‘
გრადუსი |
α2‘
რადიანი
|
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| საშუალო მნიშვნელობები
|
|||||||
| პლასტილინი | N | α1
გრადუსი |
α1
რადიანი |
α1‘
გრადუსი |
α1‘
რადიანი |
α2‘
გრადუსი |
α2‘
რადიანი |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| საშუალო მნიშვნელობები
|
|
გამოყენებული ლიტერატურა:
- ქუთაისი ტექნიკური უნივერსიტეტი
ზ. ლომთაძე, ნ. ახვლედიანი, ჯ. მეტრეველი – „ლაბორატორიული პრაქტიკუმი ფიზიკაში – მექანიკა“;
- გამომცემლობა „დიოგენე“, ფიზიკა, მე-9 კლასი, ქ. ტატიშვილი – მოსწავლის წიგნი.