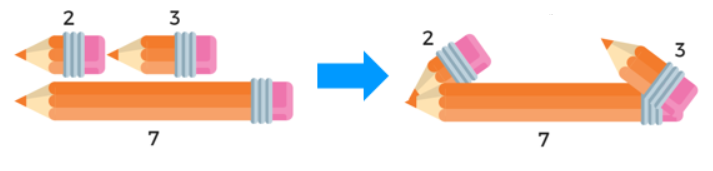
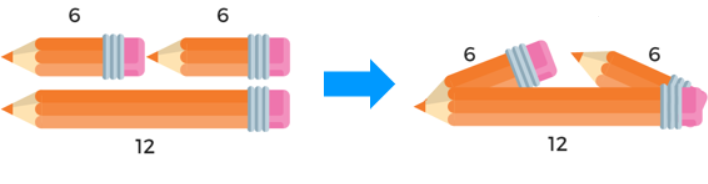
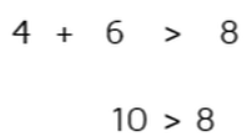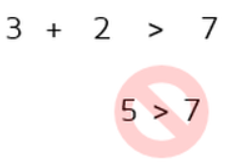„რაც მოვისმინე – დამავიწყდა, რაც დავინახე – დავიმახსოვრე, რაც გავაკეთე – გავიგე“.
ძველი ჩინური ანდაზა
ცოდნის მიღების მრავალი გზა არსებობს, შედეგად, არსებობს მრავალი მეთოდი, ტექნიკა, რომელთა სია მუდმივად ფართოვდება, ისინი იყენებენ (განსხვავებულ) კონკრეტულ უნარებს. სწავლა კეთებით კი საოცრად ეფექტური სასწავლო ინსტრუმენტია სხვადასხვა უპირატესობების გამო.
ჩვენ შეგვიძლია მოსწავლეებს ვასწავლოთ მეტი, როდესაც ისინი იძულებულნი არიან „შევიდნენ სიტუაციაში“ და ისწავლონ ის, რისი სწავლაც სჭირდებათ. ამით უფრო ადვილია გააზრება და დამახსოვრება, ყოველი ქმედება უზრუნველყოფს პერსონალიზებულ სწავლის გამოცდილებას და სწორედ აქ ყალიბდება მოტივაცია. მოტივაცია კავშირშია საკითხისადმი აქტიურ მოდგომასთან. აქტიური ჩართულობა კი უზრუნველყოფს უფრო ღრმა სწავლას.
გაგიზიარებთ მე-7 კლასში, კეთებით სწავლით მეთოდით დაგეგმილ ერთ გაკვეთილს. თეორემა სამკუთხედის უტოლობის შესახებ, არის ერთ-ერთი მნიშვნელოვანი მათემატიკური პრინციპი, რომელიც გამოიყენება სხვადასხვა დარგში, რეალურ ცხოვრებაში. სამოქალაქო ინჟინრები სამკუთხედის უტოლობის თეორემას იყენებენ ქალაქის დაგეგმარებას, ტრანსპორტირებასა და გეოდეზიაში, იგი ეხმარება მათ, გამოთვალონ უცნობი სიგრძეები და გააკეთონ სწრაფი შეფასება.
სამიზნე ცნება: გეომეტრიული ობიექტები და მათი თვისებები
კლასი: მე-7
საკითხი: სამკუთხედი
ქვესაკითხი: სამკუთხედის უტოლობა
საკვანძო შეკითხვა:
- როგორ გვეხმარება ლოგიკური მსჯელობა თეორემის დამტკიცებაში?
- როგორ ვიყენებთ სამკუთხედის უტოლობის თვისებას რეალურ ცხოვრებაში?
მიზანი: მოსწავლეები შეძლებენ, დაადგინონ, როდის შეიძლება მოცემული სიგრძის სამი მონაკვეთიდან სამკუთხედს შექმნა და როდის არ შეიძლება.
სტანდარტის მიხედვით მისაღწევი შედეგები: მოსწავლემ უნდა შეძლოს:
გეომეტრიული ობიექტების წარმოდგენა ამოცანის კონტექსტის შესაბამისად (მათ. საბ. 4,5,6);
გეომეტრიული ამოცანების ამოხსნა სამკუთხედებთან დაკავშირებული ცნებებისა და ფაქტების გამოყენებით (მათ.საბ. 1,2,3,7,8,9)
გაკვეთილის მსვლელობა
წინარე ცოდნის გააქტიურების შემდეგ პირველი აქტივობა რეალური კონტექსტის მაგალითია. მოსწავლეთა წყვილებს ვურიგებ სურათს აღწერითა და შეკითხვით.
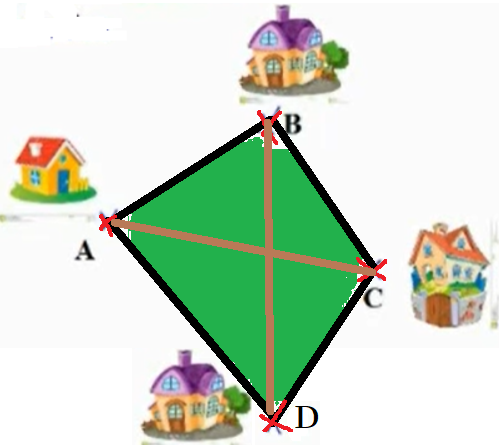
ოთხი მეგობრის საცხოვრებელი სახლები ისეა განლაგებული, როგორც სურათზე. სახლებს შორის მინდორია. სახლები ერთმანეთთან სატრანსპორტო გზითა და ფეხით მოსიარულეთათვის ტროტუარებითაა დაკავშირებული, მაგრამ მინდორზე ვხედავთ ბალახში გაცვეთილ ბილიკებს, რომლებიც დიაგონალების სახითაა მწვანესაფრიან ტერიტორიაზე. თქვენი აზრით, რატომ კვეთენ ადამიანები მინდორს A სახლიდან C სახლში მოსახვედრად და პირიქით? ან B სახლიდან D სახლში მოსახვედრად და პირიქით?
მოსწავლეები სახაზავით ზომავენ A სახლიდან C სახლში მოსახვედრ შესაძლო გზების მანძილებს. 1) AC მონაკვეთის სიგრძე, 2) AB+BC მონაკვეთების სიგრძეთა ჯამი, 3) AD+DC მონაკვეთების სიგრძეთა ჯამი. შედარებისას აღმოჩნდა AC<AB+BC, ასევე AC<AD+DC ანალოგიურად, BD<BC+CD და BD<BA+AD.
მოსწავლეებმა აღნიშნეს, რომ სწორედ ამ უტოლობების თანახმად უმოკლეს სიგრძეებს ირჩევენ A და C სახლებში მცხოვრები მეგობრები და AC ბილიკით უკავშირდებიან ერთმანეთს, ისე, რომ ზუსტი ზომების განსაზღვრა არცაა მათთვის საჭირო. იგივე ითქვა B და D სახლში მცხოვრებ მეგობრებზეც.
მოსწავლეებს ვეკითხები საინტერესოა, ეს უტოლობა ნებისმიერი სამკუთხედისთვის სრულდება, ან შეიძლება თუ არა ნებისმიერი ზომის სამი მონაკვეთით სამკუთხედის ფორმირება?
აქტივობა 2: თეორემა სამკუთხედის უტოლობის შესახებ
მიზანი: მოსწავლეები მანიპულატივების დახმარებით აღმოაჩენენ სამკუთხედის გვერდების სიგრძეების შორის დამოკიდებულებას.
მოსწავლეებს ვეკითხები: შეიძლება თუ არა სამკუთხედის ფორმირება ნებისმიერი სამი მონაკვეთით? მათი სხვადასხვა ვარაუდების შემდეგ, მივმართავ, – თავად სცადე და ნახავ!
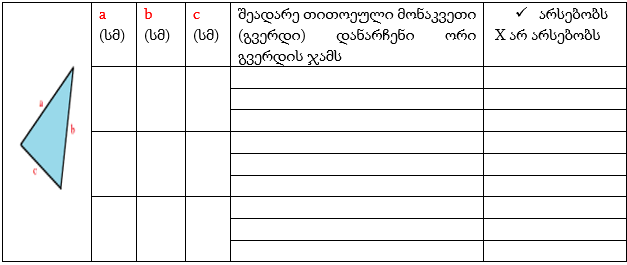
მოსწავლეებს ვურიგებ ჩხირებს, ვთხოვ ამ ჩხირებით შეკრან სამკუთხედები (ზოგ შემთხვევაში არ შედგება). შემდეგ გაზომონ ჩხირების სიგრძეები სახაზავით და აწარმოონ ცხრილი.
კლასში შეჯერდა მოსწავლეთა წყვილების ნამუშევრები. მოსწავლეები პასუხობდნენ კითხვებს, ჩხირებით ყოველთვის შეიკრა თუ არა სამკუთხედი? რა მოხდა, როცა ორი ჩხირი ძალიან მოკლე იყო და ერთი დიდი? ამდაგვარი დამხმარე შეკითხვებით, მათ მიერ ნაწარმოები ცხრილითა და მსჯელობა-ანალიზის საფუძველზე მოსწავლეებმა თავად გამოიტანეს დასკვნა: სამკუთხედის ფორმირებისთვის ერთი გვერდის სიგრძე ყოველთვის ნაკლები უნდა იყოს დანარჩენი ორი გვერდის სიგრძეთა ჯამზე, ამის შემდეგ ვთხოვე მოსწავლეებს, ეს წინადადება „თუ – – -, მაშინ – – -„ ფორმატში გადაიტანონ.
გიზიარებთ, მოსწავლეთა მუშაობის ამსახველ რამდენიმე ფოტოს.
აქტივობა 3. განმტკიცების პროცედურა
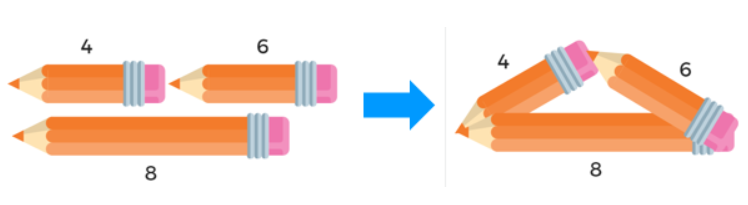
ეს აქტივობა მთელ კლასთან გავაკეთე სამი განსხვავებული შემთხვევის განხილვით. მოსწავლეებს ვეკითხები, მოცემული სიგრძის გვერდებით შესაძლებელია თუ არა სამკუთხედის შედგენა? ისინი ასაბუთებენ პასუხს, სამკუთხედის უტოლობის თეორემის გამოყენებით, ბოლოს კი მეტი თვალსაჩინოებისათვის ვაჩვენებ ვიზუალურ წარმოდგენას. ვაძლევ უკვე წინასწარ გამზადებულ ფიქსირებული ზომის ფანქრებს მოხალისე მოსწავლეს და ის მთელ კლასს კიდევ ერთხელ აჩვენებს, შედგა თუ არ სამკუთხედი.
ამ აქტივობით გავაკეთე წინა აქტივობის რეზიუმე, ამავდროულად პროცედურამ ხელი შეუწყო საკითხის უკეთ გააზრება/განმტკიცებას.
აქტივობა 4: გასასვლელი ბარათები-მოკლე წერა
ინდივიდუალური ბარათები, რომლებსაც მოსწავლეებს ვურიგებ, ამოწმებს რამდენად გაიაზრეს საკითხი და შეუძლიათ თუ არა პრობლემის დამოუკიდებლად გადაჭრა, სამკუთხედის თეორემის გამოყენებით.
გაგიზიარებთ რამდენიმე ბარათს:
| 1 | შესაძლებელია თუ არა სამკუთხედის შედგენა შემდგი ზომის გვერდებით: 7 ერთეული, 4 ერთეული და 5 ერთეული.
|
| 2 | გიორგის აქვს სამი განსხვავებული ზომის ჯოხი: 12 სმ, 20 სმ და 32 სმ. შეძლებს ის ამ ზომის ჯოხებით სამკუთხედის „გაკეთებას“?
|
| 3 | შესაძლებელია თუ არა, სამკუთხედის გვერდების სიგრძეები იყოს შემდეგი სამი რიცხვი 7; 2; 11.
|
გასასვლელი ბარათების ანალიზის საფუძველზე დავგეგმე მომდევნო გაკვეთილი.
საბოლოოდ მოსწავლეები აჯამებენ გაკვეთილის მსვლელობას, რა მოეწონათ, რა გაუმარტივდათ, შეძლებენ თუ არა გაკვეთილზე გადაჭრილი პრობლემების ანალოგიით მსგავსის დამოუკიდებლად გადაჭრას და მცირე კვლევის დამოუკიდებლად დაგეგმვას?
მოსწავლე. რომელიც სკოლაში არ იყო გადავუგზავნე ხანის აკადემიის ვიდეო სამკუთხედის უტოლობაზე ბმულის სახით, შესაბამისი სავარჯიშოებით.
საშინაო დავალება:
- სამკუთხედის გვერდების სიგრძეების წესზე ხანის აკადემიის სავარჯიშოები
- აწარმოვე კვლევა:
დახაზე რამდენიმე სახის სამკუთხედი. გაზომე გვერდები, კუთხეები. შექმენი ამ მონაცემების დასაორგანიზებელი ცხრილი, დააკვირდი გვერდის ზომასა და მის წინ მდებარე კუთხის ზომებს შორის კავშირებს და აღმოაჩინე მიმართებები სამკუთხედის გვერდებსა და შიდა კუთხეებს შორის. გამოიტანე დასკვნა. წარმოადგინე კლასის წინაშე
ამ თემას აქვს მტკიცებულება, რომლის სწავლა შესაძლებელია აღმოჩენის გზით. მოსწავლეები აცნობიერებენ, რომ მათ შეუძლიათ, რეალურად გაარკვიონ სამი მოცემული ხაზი ქმნის თუ არა სამკუთხედს. ამ საკითხის გააზრების შემდეგ მარტივია სამკუთხედების აგების ამოცანებზე მუშაობა.
გამოყენებული ლიტ-რა:
- ეროვნული სასწავლო გეგმა
- მათემატიკის გზამკვლევი მე-7 კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში.
https://math.ge/meshvide-klasi/;