ახლახანს ჩემმა საყვარელმა ლექტორმა ლატარიაში ჯეკპოტი მოხსნა. გულწრფელად ვულოცავ მას ამ მოგებას. ვის არ გვინდა, ქუდბედიანი ადამიანების მსგავსად გაგვიმართლოს, მაგრამ ლატარიაში მოგებას ყველანი მაინც შემთხვევითობას, იღბალს ვაბრალებთ და არავინ ვიტყვით, რომ ლატარიების რიცხვების ამოცნობას ლოგიკა სჭირდება. მიუხედავად ამისა, გადავწყვიტე, საკითხი მათემატიკოსებთან გამერკვია, ჰოდა, ერთობლივი გაკვეთილის ამ თემაზე ჩატარების იდეაც მაშინ გაჩნდა. გაკვეთილის ბოლოს მოსწავლეებმა უნდა უპასუხონ ჩემს შეკითხვას, რა შანსი მაქვს, ერთ-ერთი მორიგი გამარჯვებული ვიყო მეც (პირობითად). სინამდვილეში კი მე და პეტრეს გვინდა, გაკვეთილის ჩატარების შემდეგ მოსწავლეები დაფიქრდნენ, რამდენად სანდოა ინტუიცია და ღირს თუ არა ფულის გამეტება ლატარიის ბილეთების საყიდლად და საერთოდ, ღირს თუ არა ფულზე თამაში ამისთვის განკუთვნილ ნებისმიერ დაწესებულებაში.
ერთხელ სოკრატე, საკუთარი ნების წინააღმდეგ, ლამის ძალდატანებით, მიიყვანეს მდიდარი კომერსანტის კეფალეს სახლში. იმ დღეს ზღვისპირა საპორტო ქალაქი პირეოსი ერთი წლის წინ შემოსული ქალღმერთის ბენდისის დღეს აღნიშნავდა. ასეთ ღირსშესანიშნავ მოვლენას სოკრატე ვერ დააკლდებოდა, პატარა ამბავი ხომ არაა, ახალი ღვთაების შემოსვლას დააკვირდე, შენივე თვალით ნახო, დაიმკვიდრებს თუ არა ადგილს ახალი ღმერთი ტრადიციული ღმერთებით გადავსებულ ბერძნულ პანთეონში და, თუ ფეხს ვერ მოიკიდებს, ამის მიზეზებიც ახსნა. თანაც პირეოსი ათენიდან რამდენიმე კილომეტრში იყო და ის, რაც მისაღები გახდებოდა პირეოსისთვის, ათენშიც მალე გავრცელდებოდა. სადღესასწაულო ცერემონიალის დასრულების შემდეგ ასაკში შესული კეფალე მცენარეების ტოტებისგან შეკრული მსხვრეპლშეწირვისთვის დამახასიათებელი გვირგვინით დამშვენებული სავარძელში ჩამჯდარი დახვდა სოკრატეს და თავაზიანი საუბარი გაუბა ფილოსოფოსს. სოკრატეს აინტერესებს, როგორ გრძნობს თავს კეფალეს ასაკის ადამიანი, როცა სიკვდილი კართანაა მომდგარი. დამეთანხმებით, რომ ეს შეკითხვა, არცთუ ისე ზრდილობიანია; თანაც ფილოსოფოსმა ეს შეკითხვა ერთი საინტერესო დაკვირვებიდან გამომდინარე დასვა. ერთი წლის წინ შემოსულ ღვთაებას ტრადიციულ ღმერთებზე წინ არ დააყენებდა მდიდარი ადამიანი. მას ხომ ქონება ამ ძველი ღმერთების თანადგომითა და შემწეობით არ მოუპოვებია. მაგრამ კეფალეს გვირგვინი მიუთითებს, რომ მან შეწყვიტა საქმე და სახლის უკანა კარში სისხლიანი მსხვერპლშეწირვის რიტუალს მხოლოდ იმ მიზეზით მოწყდა, სოკრატეს რომ შეჰგებებოდა. სისხლიანი მსხვერპლშეწირვა საკმაოდ ძვირი ჯდებოდა, რადგან წვრილფეხა საქონლისა და ფრინველის მსხვერპლად შეწირვას გამორიცხავდა, მსხვილფეხა პირუტყვი კი ძვირი ღირდა, ამიტომ რიგით ბერძენს მისი ჩატარება გაუჭირდებოდა. სოკრატეს შეკითხვა, თავს როგორ გრძნობს კეფალე მოახლოებული სიკვდილის მოლოდინში, მიუხედავად უტაქტობისა, დროულია, რადგან პასუხის მიხედვით გაირკვევა, რომ, მდიდრებს ღარიბებთან შედარებით, სიცოცხლესთან ერთად სიკვდილიც „იოლი“ ჰგონიათ. კეფალეს პასუხი ამ მოსაზრების ნათელი მაგალითია. კეფალე ამბობს, რომ მისთვის სამართლიანია, ყველას თავისი კუთვნილი მიეგოს, ადამიანმა მიიღოს ის, რაც მას ერგება, ღმერთებმაც – ასევე. ნათქვამი ასე უნდა გავიგოთ: სანამ სიკვდილი კარზე მოგვიკაკუნებს, ადამიანებს ვალები უნდა დავუბრუნოთ, ღმერთებს კი არ უნდა ვაწყენინოთ და მსხვერპლი შევწიროთ, სულ ერთია, დიდი ღვთაება იქნება ეს თუ მცირე, თუნდაც ერთი წლის წინ მცირე აზიიდან შემოსული ბენდისი. მდიდარ კომერსანტ კეფალეს ქონება აქვს და იგი მზადაა, ამ ქონების ნაწილი თამამად დახარჯოს და ღმერთების გული იქამდე მოიგოს, სანამ სიკვდილი წაიყვანს. იმ ქვეყანაში კი, ვაიდა, მართალია ამბები, რომლებსაც მიწისქვეშეთზე ჰყვებიან, წელგამართული გადავიდეს და ისეთივე ღირსეული ადგილი დაიმკვიდროს, როგორიც მას, ფულის წყალობით, სააქაოში აქვს.
ალბათ ბევრს გეცნოთ მდიდარი კაცის განწყობა. ეს განწყობა საუკუნეებია არსად გამქრალა და დღემდე გრძელდება, მხოლოდ რელიგიების დასახელებები და ღმერთების სახელები შეიცვალა. ამის მიზეზი კი ადამიანის ინტუიციაა. ამბობენ, სამი ტიპის ინტუიცია არსებობსო: საგნის ცოდნაზე დაფუძნებული, სოციალური და ძირეული. საგნის ცოდნაზე (აქ აკადემიურ საგანს არ ვგულისხმობთ) დაფუძნებული ინტუიციაა ბიზნესმენების ინტუიცია, როდესაც ალღოთი გრძნობენ, როდისაა მოქმედება დროული. საგნის ცოდნაზეა დამოკიდებული მეცნიერული ალღოც, დედის გრძნობა, როდის გახდება შვილი ავად და მასწავლებლის უტყუარი ალღოც, როდის არ იცის მოსწავლემ გაკვეთილი; სოციალური ინტუიცია ადამიანის უნარია, გარეგნობის, საქციელის მიხედვით იმსჯელოს სხვა ადამიანებზე და იწინასწარმეტყველოს, ვინ როგორ მოიქცევა ამა თუ იმ სიტუაციაში; აი ძირეული ინტუიცია კი მეტაფიზიკურ ცოდნას ეფუძნება – ხვალ რომ დედამიწის გრავიტაცია არ დაირღვევა და ფრენას არ დავიწყებთ, მზე რომ ცაზე „მოძრაობას“ გააგრძელებს, სიცოცხლე რომ სიზმარი არაა, მსგავსი ტიპის „ცოდნა“ ძირეულ ინტუიციას განეკუთვნება. ადამიანის ღმერთების მიმართ კეფალესმაგვარი დამოკიდებულება, რომელიც საუკუნეებია გრძელდება, სწორედ ძირეული ინტუიციის ბრალია.
ამ ინტუიციის შესახებ იცოდა პასკალმაც, უდიდესმა მოაზროვნემ და გამორჩეულმა მეცნიერმა, ღრმად მორწმუნე ქრისტიანმა-იანსენისტმა. მან ისიც იცოდა, რომ ინტუიცია არადამაჯერებელი არგუმენტია და გადაწყვიტა, ინტუიცია ლოგიკით, ლოგიკაზე დაფუძნებული მსჯელობით ანუ ბევრად უფრო უტყუარი და სანდო მტკიცებულებით, გაემყარებინა. პასკალი შეეცადა, ლოგიკა გამოეყენებინა იმ სფეროში, რომელშიც, ტრადიციულადაა მიჩნეული, რომ მისი ადგილი იქ არ არის.
არგუმენტს, რომელიც პასკალმა მოიფიქრა, პასკალის ნაძლევს უწოდებენ. პასკალი ამბობს, დავუშვათ ორი ვარიანტი. ერთის მიხედვით, ღმერთი არსებობს, მეორეს მიხედვით, კი ღმერთი არ არსებობს. ამის შემდეგ წარმოვიდგინოთ, როგორი იქნება ურწმუნო და მორწმუნე ადამიანის ამქვეყნიური და იმქვეყნიური ცხოვრება. თუკი ადამიანი ამ ქვეყანაზე ღვთაებრივ კანონებს დაარღვევს, ღმერთის არარსებობის შემთხვევაში მას არაფერი ემუქრება, ხოლო ღმერთის არსებობის შემთხვევაში სასტიკი სასჯელი ელის. თუკი ადამიანი ღვთაებრივი კანონებით ცხოვრობს, გარდაცვალების შემთხვევაში ვერანაირ ჯილდოს ვერ მიიღებს, თუკი ღმერთი არ არსებობს; სამაგიეროდ, მოგებული დარჩება, თუკი ღმერთი არსებობს. ამიტომაც, პასკალის აზრით, ყველა შემთხვევაში უმჯობესია (რადგან მას ჯილდო მოაქვს), ღმერთი არსებობდეს და ადამიანიც მორწმუნე იყოს. ცხადია, პასკალთან ბევრი პრეტენზია ჰქონდათ ამ არგუმენტის გამო, მაგრამ ეს არგუმენტი გასაგებია მათთვის, ვინც ალბათობის თეორიას იცნობს.
| ღმერთი არ არსებობს | ღმერთი არსებობს | |
| ურწმუნო | არაფერი | სასჯელი |
| მორწმუნე | არაფერი | ჯილდო |
ახლა ვნახოთ, რას გულისხმობს ალბათობის თეორია და როგორ მუშაობს იგი მათემატიკაში. მათემატიკის სახელმძღვანელოებში ვაწყდებით ალბათობის ამოცანებს. უმეტესად ეს ამოცანები ეხება ყუთიდან სხვადასხვა ფერის ბურთების ან რაიმე ნივთების შემთხვევითი ამორჩევის პრინციპით კომბინაციების დათვლას -რამდენად სასარგებლოა ეს რეალურ ცხოვრებაში? თუმცა ალბათობის თეორიას აქვს გასაკვირი გამოყენებებიც – პასუხები მგძნობიარე კითხვებზე. ადამიანები ზარალდებიან, როცა არასწორად იყენებენ მას ან ვერ იგებენ ალბათობას და ეყრდნობიან საკუთარ ინტუიციას ნაცვლად იმისა, რომ დათვალონ და შეაფასონ შანსები. მოდით, გავშალოთ ეს საკითხები. დავსვათ შეკითხვა: რატომ ყიდულობენ ადამიანები ლატარიის ბილეთებს, როდესაც მოგების შანსები საკმაოდ მცირეა ? რა არის ალბათობა იმისა, რომ თქვენ მოიგებთ ლატარიას ? ჯერ განვიხილოთ ალბათობის თეორიის ცნობილი ამოცანა დაბადების დღის პრობლემის შესახებ. კლასში 23 მოსწავლეა. რა არის ალბათობა იმისა, რომ ორ მოსწავლეს დაბადების დღე ჰქონდეს ერთსა და იმავე დღეს ? რას ფიქრობთ, რა არის პასუხი? 1%? შეიძლება 5%? ან თუნდაც მთელი 10%? გამოვიყენოთ მათემატიკა ამის დასადგენად: 23 სტუდენტი ნიშნავს 253 მოსწავლეთა წყვილს: (23×22)÷2=253. ალბათობა, რომ დაბადების დღე ორ მოსწავლეს ექნება განსხვავებულ დღეს არის 364÷365=0.997260. ხოლო 253 წყვილისათვის იმის ალბათობა, რომ თითოეულ წყვილში დაბადების დღე ექნებათ განსხვავებულ დღეს, იქნება (364÷365)253 =0.4995. მაშასადამე, ალბათობა იმისა, რომ 253 წყვილში ორ ადამიანს წყვილში ექნებათ ალბათობა ერთსა და იმავე დღეს, იქნება: 1-0.49995=0.5005 ან 50.05%, რაც აშკარად ეწინააღმდეგება ჩვენს ინტუიციას.
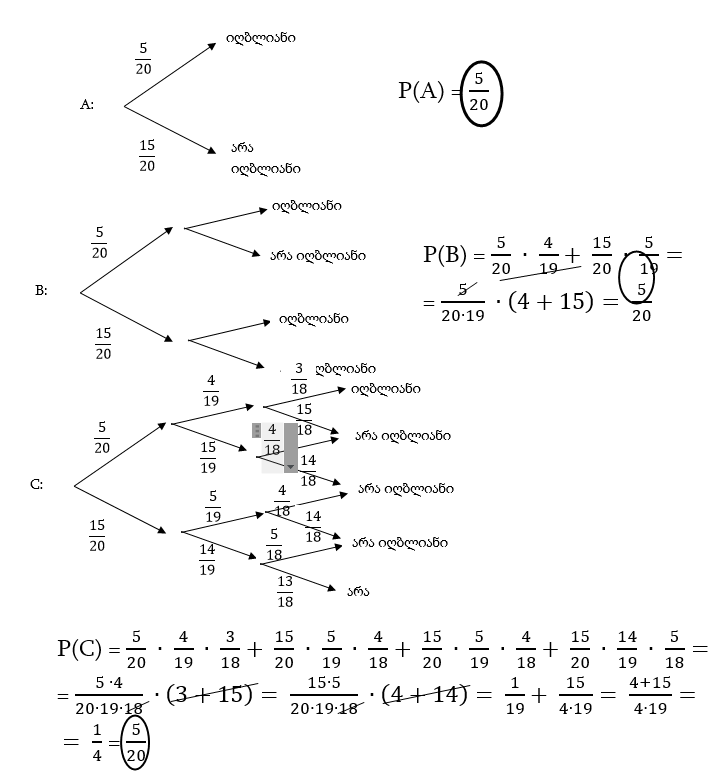
განვიხილოთ კიდევ ერთი მაგალითი, როცა ინტუიცია ეწინააღმდეგება ჭეშმარიტებას. დავსვათ შემდეგი ამოცანა: გვაქვს 20 საგამოცდო საკითხი და ამ 20 საკითხში 5 საკითხი არის ე. წ. იღბლიანი საკითხი. ვთქვათ A, B და C მოსწავლეები რიგ-რიგობით მიდიან საკითხის ასაღებად, რომელს უფრო მეტი შანსი (ალბათობა) აქვს იღბლიანი საკითხის შეხვედრის A, B თუ C მოსწავლეს? ამ შეკითხვის დასმის შემდეგ პასუხები არ დააყოვნებს და უმრავლესობა ინტუიციაზე დაყრდნობით იტყვის შემდეგ თანმიმდევრობას: A, B,C, ე.ი. იღბლიანი ბილეთის აღების ყველაზე დიდი შანსი პირველ მოსწავლეს აქვს, ხოლო ყველაზე ნაკლები – მესამეს. მოდით ახლა უკვე რეალურად, ლოგიკურ მსჯელობაზე დაყრდნობით, შევაფასოთ თითოეული მოსწავლისთვის იღბლიანი საკითხის შეხვედრის ალბათობა. ამოხსნის შემდეგ მივიღებთ სწორედ ჩვენი ინტუიციის საწინააღმდეგო პასუხს, რომ თითოეულ მონაწილე მოსწავლეს ტოლი შანსები ექნება (ამოხსნა იხ. წერილის ბოლოს)
ახლა კი შევაჯამოთ გაკვეთილი: რა არის ინტუიცია? ზოგი მას სწრაფ ლოგიკასაც უწოდებს; ინტუიციას „აჰა, მომენტი“-ც ჰქვია. ამიტომაც ბევრი ფიქრობს, რომ ის სანდო პარტნიორია სხვადასხვა საქმეში. მაგრამ ყველამ ვიცით, რომ სისწრაფე ხშირად აფუჭებს საქმეს, თუმდაც მის უკან ლოგიკა იდგეს. სისწრაფე მაშინაა კარგი, როდესაც გამოუვალ სიტუაციაში გადაწყვეტილებების მიღებაა საჭირო. ინტუიცია დიდ სამსახურს უწევდა ჩვენს წინაპრებს სხვადასხვა საქმიანობაში, იქნებოდა ეს ნადირობა თუ ბრძოლა; ინტუიცია ეხმარებოდა დიდ მეცნიერებს, პასუხისთვის მიეგნოთ. მაგრამ იმ საქმეში, სადაც დაფიქრება შეიძლება, სადაც დრო არის ავწონ-დავწონოთ დადებითი და უარყოფითი მხარეები, აჯობებს, ლოგიკაზე დაფუძნებული გადაწყვეტილებები მივიღოთ. რადგან არავინ იცის, სანამ ინტუიცია გაგვიმართლებს, რამდენ ალოგიკურ საქცილეს ჩავიდენთ.
გაკვეთილის ბოლოს მივცეთ მოსწავლეებს ამოცანა (ლატარიის ბილეთზე 36 ციფრია და უნდა შემოიხაზოს 6 სასურველი ციფრი. რამდენია ბილეთით მოგების ალბათობა) და მიღებულ შედეგზე დაფუძნებული პასუხით გვირჩიონ, რამდენად გვიღირს და რამდენად არ გვიღირს ფულის, თუნდაც მცირე თანხის, დახარჯვა ლატარიის ბილეთზე.