სასკოლო მათემატიკის პროგრამა ხშირად გვაიძულებს “სწრაფად და ფართოდ” მოქმედებას– მოკლე დროში ბევრი თემის ზედაპირულად გავლას. შედეგად, რთული, მაგრამ ფუნდამენტური საკითხები, როგორიცაა სინუსოიდური ფუნქციების მოდელირება, ხშირად იქცევა მხოლოდ მექანიკური დამახსოვრების საგნად. მოსწავლეები სწავლობენ გრაფიკების აგებას, მაგრამ ვერ აცნობიერებენ, რატომ არის კრიტიკულად მნიშვნელოვანი პარამეტრები A, B, C და D.
მე-11 კლასში ჩატარებული ჩემი გაკვეთილის მთავარი მიზანი სწორედ ამ პედაგოგიური დილემის გადაჭრა იყო: ფორმულების მექანიკური დამახსოვრების სიღრმისეული გაგებით ჩანაცვლება. მიუხედავად იმისა, რომ მან დიდი დროს მოითხოვა. გაკვეთილი, რომელიც თავისი მოცულობით 3-4 საგაკვეთილო საათს მოიცავდა, სცილდებოდა სტანდარტული დროის ლიმიტს, მაგრამ დამანახა, რომ სინუსოიდური ფუნქციებისის y(t) = A sin(B(t-C)) + D; y(t) = Acos(B(t-C)) + D თითოეული პარამეტრის ინტენსიური, კონტექსტის შესაბამისი კვლევა (ამპლიტუდა, პერიოდი, ფაზური და ვერტიკალური წანაცვლება) სრულად ამართლებს დროის ინვესტიციას.
ამ სტატიაში გაგიზიარებთ ჩემს გამოცდილებას, თუ როგორ იქცა მათემატიკის აბსტრაქტული თემა – „რხევითი მოძრაობის მოდელირება“ საკვლევ საკითხად, რითაც მოსწავლეებმა მიაღწიეს საკითხის გააზრების მაღალ ხარისხს, რომელსაც მხოლოდ ზედაპირული გავლა ვერ უზრუნველყოფდა. სტატიაში დეტალურად განვიხილავ გაკვეთილის სტრუქტურას, გამოყენებულ მეთოდებსა და კონკრეტულ შედეგებს.
მიმართულება: ალგებრა და კანონზომიერება
თემატური ბლოკი: შესაბამისობა, გრაფიკი, დამოკიდებულება, ფუნქცია
ძირითადი საკითხები: ტრიგონომეტრიული ფუნქციები და პერიოდული მოვლენები
- პერიოდული მოვლენების აღმწერი ფუნქციების გრაფიკების განხილვა; ფუნქციის პერიოდულობა და პერიოდი;
- ტრიგონომეტრიული ფუნქციები და მათი გრაფიკები – მარტივი ნიმუშების განხილვა; ( ; ;
- და ფუნქციების გარდაქმნებით მიღებული გრაფიკები, მათ შორის ფაზით წანაცვლება; სხვადასხვა პერიოდის, სიხშირისა და ამპლიტუდის მქონე ჰარმონიული რხევები;
- რეალური სიტუაციის მოდელირება და პრობლემის გადაჭრა ფუნქციისა და გრაფიკის საშუალებით;
- ფუნქციის გამოყენება სხვადასხვა კონტექსტში ცვლილებათა გასაანალიზებლად და რეალური მოვლენების მოდელირებისთვის.
| სამიზნე ცნებები | ||
| 1. მათემატიკური მოდელი | 2. კანონზომიერება | 3. ლოგიკა |
| რეალური პერიოდული მოვლენების (ტალღა, ტემპერატურა) აღსაწერად y(t) = A sin(B(t-C)) + D ფორმულის საშუალებით რეალური სიტუაციის მოდელირება და მომავალი მდგომარეობის გამოთვლა. | პერიოდული მოვლენების და მათი აღმწერი ფუნქციების გრაფიკების განხილვა. პარამეტრების (A, B, C, D) კვლევა/ანალიზი. | ფუნქციური დამოკიდებულებებისა და ტრიგონომეტრიული იგივეობების ანალიზი. მსჯელობა: ლოგიკური დასკვნების გამოტანა. (მიზეზ-შედეგობრივი კავშირი პარამეტრებსა და გრაფიკს შორის). |
მათემატიკის სტანდარტის შედეგები:
მათ.საშ.3.: შესასწავლი მოვლენიდან გამომდინარე ცვლად თუ მუდმივ სიდიდეთა შორის შესაბამისობის, ფუნქციური კავშირის დამყარება და წარმოდგენა შესაბამისი ერთი ან რამდენიმე ფორმით; ფუნქციის გამოყენება სხვადასხვა კონტექსტში ცვლილებათა გასაანალიზებლად და რეალური მოვლენების მოდელირებისთვის.
გაკვეთილის მსვლელობა ( 3-4 საგაკვეთილო საათი)
აქტივობა1. პარამეტრი A; ამპლიტუდა.
თემა: გრაფიკის ვერტიკალური გაჭიმვა/შეკუმშვა:
მიზანი: ემპირიულად (ცდით) აღმოაჩინონ, რომ y = A sinx ფუნქციაში A პარამეტრი აკონტროლებს ტალღის სიმაღლეს (ამპლიტუდას).
საჭირო რესურსი: კომპიუტერი/ტაბლეტები ინტერნეტით, ონლაინ გრაფიკული კალკულატორი (Desmos ან GeoGebra).
მსვლელობა:
- საკვანძო შეკითხვა: (ცხოვრებისეული კავშირი) წყნარ ოკეანეში მოქცევის სიმაღლე გაცილებით მეტია, ვიდრე შავ ზღვაში? რა იცვლება მათ გრაფიკებში.
- ბაზისური მოდელის ანალიზი:
- მოსწავლეებმა ააგეს ბაზისური გრაფიკი: y = sin(x)
- დაადგინეს მაქსიმალური და მინიმალური მნიშვნელობებია y=1 და y=-1.
- ჰიპოთეზის წამოყენება
- კითხვა: თუ A კოეფიციენტს გავზრდით, მაგალითად A=3-ზე, გრაფიკი გაიჭიმება თუ შეიკუმშება?
- მოსწავლეებმა დაწერეს თავიანთი ვარაუდები.
- ცდის ჩატარება და მონაცემთა შეგროვება:
მოსწავლეებმა ჯგუფებში, გრაფიკული კალკულატორის (Desmos ან GeoGebra) გამოყენებით ააგეს ფუნქციების გრაფიკები და შეავსეს შემდეგი ცხრილი
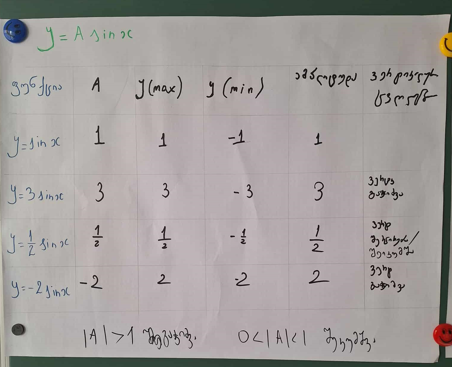
| ფუნქცია | A-ს მნიშვნელობა | მაქსიმალური | მინიმალური ( | ამპლიტუდა A | აღმოჩენა: ვერტიკალური ცვლილება |
| y = sin(x) | A=1 | 1 | -1 | 1 | ბაზისური |
| y = 3sin(x) | A=3 | ? | ? | ? | ? |
| y = 1/2sin(x) | A=1/2 | ? | ? | ? | ? |
| y = -2sin(x) | A=-2 | ? | ? | ? | ? |
 |
 |
5. მონაცემთა ანალიზი და დასკვნის ჩამოყალიბება
მოსწავლეები გაანალიზეს და შეადარეს შედეგები, თუ როგორ უკავშირდება კოეფიციენტი A ტალღის სიმაღლეს: მაგალითად, როდესაც A=3, მაქსიმალური მნიშვნელობა გახდა 3 და მინიმალური -3. როდესაც A=1/2, გრაფიკი ვერტიკალურად შეიკუმშა.
ამ კვლევის საფუძველზე, მოსწავლეებმა ჩამოაყალიბეს წესი:
- როდესაც ამპლიტუდის აბსოლუტური მნიშვნელობა |A| > 1 -ზე ფუნქციის გრაფიკი გაჭიმულია ვერტიკალურად.
- როდესაც A-ს აბსოლუტური მნიშვნელობა 0-სა და 1-ს შორისაა, 0 < |A| < 1 გრაფიკი შეკუმშულია ვერტიკალურად
- შეჯამება და ცხოვრებისეული კავშირი:
განიხილეს ამპლიტუდის როლი რეალურ მოვლენებში:
როგორ მოქმედებს ამპლიტუდა ხმაზე? (რაც მეტია ამპლიტუდა, მით უფრო ხმამაღალია ბგერა). როგორ მოქმედებს სინათლეზე? (რაც მეტია ამპლიტუდა, მით უფრო კაშკაშაა სინათლე).
აქტივობა2: პარამეტრი B და პერიოდის ცვლილება.
თემა: გრაფიკის ჰორიზონტალური შეკუმშვა/გაჭიმვა
მიზანი: ემპირიულად (ცდით) აღმოაჩინონ, რომ y = A sin(Bx) ფუნქციაში B პარამეტრი მოქმედებს პერიოდზე (T), ფორმულით
საჭირო რესურსი: კომპიუტერი/ტაბლეტები ინტერნეტით, ონლაინ გრაფიკული
კალკულატორი (Desmos ან GeoGebra).
მსვლელობა:
- ბაზისური მოდელის გახსენება:
გავიხსენეთ y = sin(x) ფუნქციის ძირითადი პარამეტრები.: ამპლიტუდა (=1) და პერიოდი (T=2π 6.28).
- ბაზისური გრაფიკის ანალიზი:
- მოსწავლეებმა ონლაინ კალკულატორში ააგეს ბაზისური გრაფიკი: y = sin(x).
- დაადგინეს, რომ ერთი სრული ტალღა სრულდება x 28 (2π) წერტილში.
- ჰიპოთეზის წამოყენება.
- კითხვა: თუ B კოეფიციენტს გავზრდით, მაგალითად B=2, მაშინ გრაფიკი გაიჭიმება თუ შეიკუმშება?
- მოსწავლეებმა დაწერეს თავიანთ ვარაუდებს.
- ცდის ჩატარება და მონაცემთა შეგროვება:
მოსწავლეებმა ჯგუფებში, გრაფიკული კალკულატორის (Desmos ან GeoGebra) გამოყენებით ააგეს ფუნქციების გრაფიკები და შეავსეს შემდეგი ცხრილი
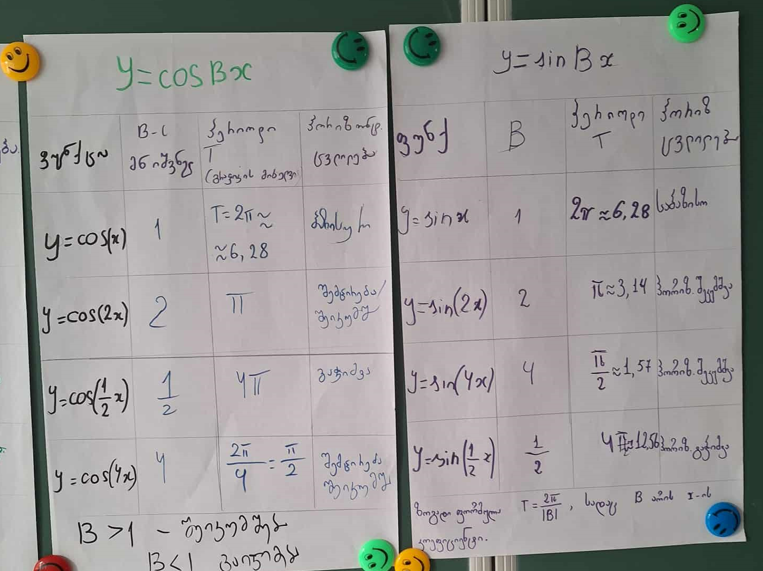
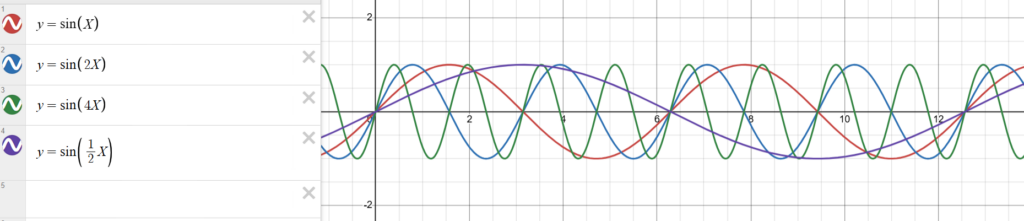
| ფუნქცია | B-ს მნიშვნელობა | პერიოდი (T) გრაფიკის მიხედვით | აღმოჩენა: შეკუმშვა/გაჭიმვა |
| y =sin(x) | B=1 | 2π 6.28 | ბაზისური |
| y = sin(2x) | B=2 | T = ? | ? |
| y = sin(4x) | B=4 | T = ? | ? |
| y = sin(1/2x) | B=1/2 | T = ? | ? |
 |
 |
5. მონაცემთა ანალიზი და დასკვნის ჩამოყალიბება
მოსწავლეებმა შეადარეს შედეგები:
როდესაც B=2, პერიოდი გახდა π(3.14).
როდესაც B=4, პერიოდი გახდა (1.57).
როდესაც B= , პერიოდი გახდა 4π (12.56).
დასკვნის ჩამოყალიბებისათვის მოსწავლეებს დავუსვი კითხვა: -როგორ შეგვიძლია B-ს მნიშვნელობა გადავაქციოთ პერიოდის (T) მნიშვნელობად? მოსწავლეებმა მარტივად აღმოაჩინეს კანონზომიერება, რომ .
5. შეჯამება და ცხოვრებისეული კავშირი
განიხილეს B პარამეტრის როლი ტალღებში (პერიოდული მოვლენების კონტექსტში, როგორ უკავშირდება ეს ტალღებს?) ვისაუბრეთ სიხშირეზე: რაც მეტია B კოეფიციენტი, მით მაღალია ტალღის სიხშირე (ბევრი ციკლი მცირე დროში). რაც B და T-ს შორის უკუპროპორციულ დამოკიდებულებას ადასტურებს.
აქტივობა 3. სავარჯიშოების შესრულება. პარამეტრების (A და B) განმტკიცება
აქტივობა 3 მოიცავდა სავარჯიშოების სერიას. მოსწავლეებმა ეს დავალებები ჯერ ინდივიდუალურად შეასრულეს, შემდეგ კი მთელ კლასთან ერთად განიხილეს. აქტივობის მთავარი მიზანი იყო A და B პარამეტრების გამოთვლის უნარის განმტკიცება და საწყისი ცოდნის გამყარება. ამისათვის მოსწავლეებმა გამოიყენეს ინტეგრირებული მსჯელობა ფუნქციის ჩანაწერის y = A sin(Bx) სწრაფი ანალიზისთვის, რათა მკაფიოდ გაერჩიათ ვერტიკალური გაჭიმვა/შეკუმშვა (ამპლიტუდა) და ჰორიზონტალური გაჭიმვა/შეკუმშვა (პერიოდი).
| #1. განსაზღვრეთ ფუნქციის პერიოდი
#2. განსაზღვრეთ ფუნქციის პერიოდი g #3. რას უდრის ამპლიტუდა ? ფუნქცია ვერტიკალურად არის გაჭიმული თუ შეკუმშული? #4. რას უდრის ამპლიტუდა ? ფუნქცია ვერტიკალურად არის გაჭიმული თუ შეკუმშული?
|
A და B პარამეტრების კვლევის დასრულების შემდეგ, რაც ფუნქციის ფორმაზე (ვერტიკალური და ჰორიზონტალური გაჭიმვა/შეკუმშვა) ფოკუსირდებოდა და რასაც შესაბამისი სავარჯიშოების განმტკიცება მოჰყვა, გადავედით გაკვეთილის შემდეგ ეტაპზე. ეს ეტაპი მოიცავდა ფუნქციის განლაგების საკითხს – კერძოდ, ჰორიზონტალური (ფაზური) წანაცვლების (C) და ვერტიკალური წანაცვლების (D) კვლევითი გაკვეთილის დაგეგმვას.
აქტივობა 4: პარამეტრი C (ფაზური წანაცვლება).
თემა: ფუნქციის ჰორიზონტალური წანაცვლება:
ფუნქციის ფორმა: y = A sin(B(x – C))
მიზანი: ემპირიულად აღმოაჩინონ, რომ C პარამეტრი მთელ გრაფიკს გადაადგილებს ჰორიზონტალურად და რომ ფაზური წანაცვლების მიმართულება საპირისპიროა ნიშნის მიმართ.
საჭირო რესურსი: ონლაინ გრაფიკული კალკულატორი (Desmos ან GeoGebra).
მსვლელობა:
- შესავალი: (ცხოვრებისეული კავშირი)
წარმოვიდგინოთ ტალღები: -რა მოხდება, თუ მოქცევის დროის თუ გაზომვას დავიწყებთ 3 საათის დაგვიანებით? ტალღა იგივე იქნება, მაგრამ მისი დაწყების დრო შეიცვლება?
- ბაზისური გრაფიკის ანალიზი:
- მოსწავლეები აგებენ ბაზისურ გრაფიკს: y= sin(x)
- დაადგინეს, რომ ბაზისური გრაფიკი იწყება (0, 0)-დან.
- ჰიპოთეზის წამოყენება
- კითხვა: -თუ x-ს გამოვაკლებთ π/2-ს, = sin(x – π/2), გრაფიკი წავა მარჯვნივ თუ მარცხნივ?
- მოსწავლეები წერენ თავიანთ ვარაუდებს.
- ცდის ჩატარება:
მოსწავლეებმა ჯგუფებში, გრაფიკული კალკულატორის (Desmos ან GeoGebra) გამოყენებით ააგეს ფუნქციების გრაფიკები და შეავსეს შემდეგი ცხრილი
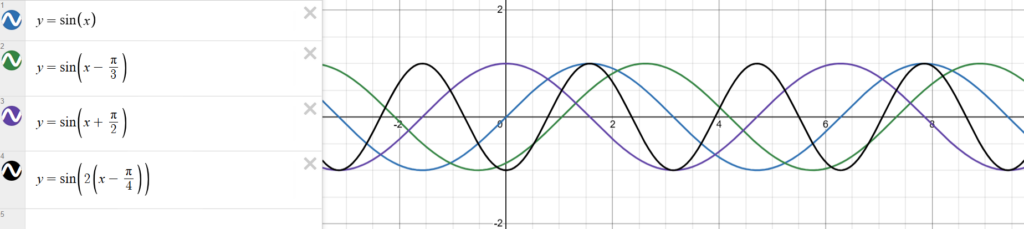
| ფუნქცია | C-ს მნიშვნელობა | საწყისი წერტილი (0, 0) | წანაცვლების მიმართულება | ჰორიზონტალური ცვლილება |
| y = sin(x) | C=0 | (0, 0) | ბაზისური | ბაზისური |
| y = sin(x – π/3) | C=π/3 | ? | ? | ? |
| y = sin(x + π/2) | C=-π/2 | ? | ? | ? |
| y = sin(2(x – π/4)) | C=π/4 | ? | ? | ? |
 |
 |
5. მონაცემთა ანალიზი და დასკვნის ჩამოყალიბება
მოსწავლეებმა შეადარეს შედეგები და გამოიტანეს დასკვნა:
ფაზური წანაცვლება C ყოველთვის საპირისპიროდ მოქმედებს ნიშანზე:
- x – C (მინუსი) წანაცვლება მარჯვნივ (პლუს მიმართულებით)
- x + C (პლუსი) წანაცვლება მარცხნივ (მინუს მიმართულებით)
წესის დასაბუთება: ფაზური წანაცვლება არის C ერთეულით და მისი მიმართულება არის საპირისპირო C-ს ნიშნის მიმართ, რადგან ფუნქციის ნული წერტილი ნაპოვნია განტოლებით x-C=0-ზეა (x=C)
- შეჯამება და ცხოვრებისეული კავშირი :
ფაზური წანაცვლება არის დროის დაგვიანება პერიოდულ მოვლენაში. გამოიყენება: ფაზური წანაცვლება აქტიურად გამოიყენება ინჟინერიაში, სადაც სხვადასხვა ტალღის სიგნალი უნდა იყოს ფაზაში (მაგალითად, სამფაზიანი დენი).
როდესაც დასრულდა A, B და C პარამეტრების კვლევა, გადავიდით ბოლო პარამეტრზე: ვერტიკალურ წანაცვლებაზე (D).
აქტივობა 5: პარამეტრი D .
თემა: ფუნქციის ვერტიკალური წანაცვლება
მიზანი: ემპირიულად (ცდით) აღმოაჩინონ, რომ y = A sin(Bx) + D ფუნქციაში D პარამეტრი მთელ გრაფიკს ასწევს ან დაწევს ვერტიკალურად და განსაზღვრავს საშუალო ხაზს.
საჭირო რესურსი: კომპიუტერი/ტაბლეტები ინტერნეტით, ონლაინ გრაფიკული კალკულატორი (Desmos ან GeoGebra).
მსვლელობა:
- შესავალი (ცხოვრებისეული კავშირი):
დავუბრუნდეთ მოქცევის მაგალითს: -რა მოხდება, თუ ზღვის საშუალო დონე (რაც ნულოვანია სტანდარტულად) შეიცვლება კლიმატის გამო? ტალღები მაინც იქნება, მაგრამ სად იქნება მათი ცენტრი?
- ბაზისური გრაფიკის ანალიზი:
- მოსწავლეები აგებენ ბაზისურ გრაფიკს: y = sin(x).
- დაადგენენ, რომ საშუალო ხაზი არის y=0 (X ღერძი)
- ჰიპოთეზის წამოყენება:
- კითხვა: – თუ D კოეფიციენტს დავუმატებთ, მაგალითად +3-ს, გრაფიკი სად წავა? ზემოთ, ქვემოთ, თუ შეიცვლის ამპლიტუდას?
- მოსწავლეები წერენ თავიანთ ვარაუდებს.
- ცდის ჩატარება და მონაცემთა შეგროვება:
მოსწავლეებმა ჯგუფებში, გრაფიკული კალკულატორის გამოყენებით ააგეს ფუნქციების გრაფიკები (ამჯერად A=1 და B=1 პარამეტრების ფიქსაციით) და შეავსეს შესაბამისი ცხრილი
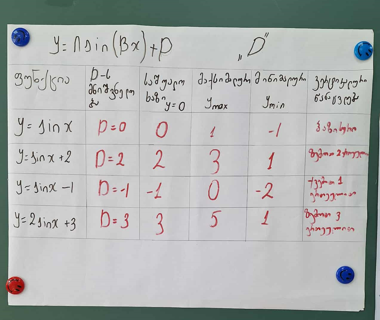
| ფუნქცია | D-ს მნიშვნელობა | საშუალო ხაზი (y=D) | მაქსიმალური | მინიმალური ( |
ვერტიკალური ცვლილება |
| y = sin(x) | D=0 | 0 | 1 | -1 | ბაზისური |
| y =sin(x) + 2 | D=+2 | ? | ? | ? | ? |
| y = sin(x) – 1 | D=-1 | ? | ? | ? | ? |
| y = 2sin(x) + 3 | D=+3 | ? | ? | ? | ? |
 |
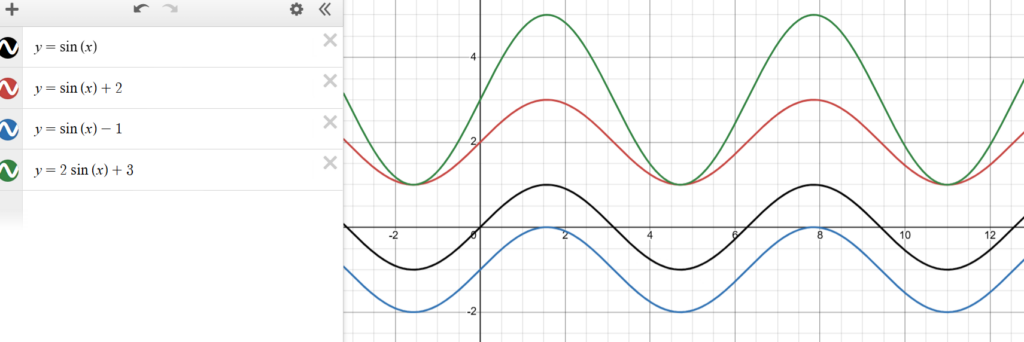 |
5. მონაცემთა ანალიზი და დასკვნის ჩამოყალიბება
მოსწავლეებმა შეადარეს შედეგები და გამოიტანეს დასკვნა:
- როდესაც D=2 (მთელი ) გრაფიკი 2 ერთეულით ავიდა ზემოთ.
- ამპლიტუდა არ შეცვლილა.
დასკვნა: აღმოჩნდა, რომ D პარამეტრი წარმოადგენს ფუნქციის საშუალო ხაზს და იწვევს გრაფიკის ვერტიკალურ წანაცვლებას
- შეჯამება და ცხოვრებისეული კავშირი :
განიხილეს D პარამეტრის როლი მოქცევის მოდელირებაში, თუ როგორ უკავშირდება D პარამეტრი მოქცევას (D არის ზღვის საშუალო დონე, რომლის ირგვლივ ტალღა აგრძელებს რხევას).
აქტივობა 6. სავარჯიშოების შესრულება. პარამეტრების (C და D) განმტკიცება
მოსწავლეებმა ეს სავარჯიშოები ჯერ ინდივიდუალურად შეასრულეს, რათა ცოდნა განემტკიცებინათ, შემდეგ კი მთელ კლასთან ერთად განიხილეს, რამაც ხელი შეუწყო ინტეგრირებული მსჯელობის განვითარებას. აქტივობის მთავარი მიზანი იყო, მოსწავლეებს განემტკიცებინათ ლოგიკური მსჯელობა წანაცვლებების მიმართულებების შესახებ და საბოლოოდ შეძლებოდათ ფუნქციის სრული ანალიზი y = A sin(B(x-C)) + D ფორმულის მიხედვით.
| #1 | განსაზღვრეთ ფაზური ცვლის მიმართულება და სიდიდე |
| #2 | განსაზღვრეთ ფაზური ცვლის მიმართულება და სიდიდე g |
| #3 | განსაზღვრეთ ვერტიკალური ცვლის მიმართულება და სიდიდე |
| #4 | განსაზღვრეთ ვერტიკალური ცვლის მიმართულება და სიდიდე |
| #5 | განსაზღვრეთ ფუნქციის შუა ხაზი, ამპლიტუდა, პერიოდი და ფაზური ცვლა
|
| #6 | განსაზღვრეთ ფუნქციის შუა ხაზი, ამპლიტუდა, პერიოდი და ფაზური ცვლა
|
აქტივობა 7 . შეჯამება და სრული ანალიზი :
მიზანი: ტრიგონომეტრიული ფუნქციის სრული ანალიზი
ამ ოთხი კვლევითი აქტივობებისა და სავარჯიშოების შესრულების შემდეგ, მოსწავლეებმა ემპირიულად აღმოაჩინეს, თუ როგორ მოქმედებს თითოეული პარამეტრი გრაფიკზე
y = A sin(B(x – C)) + D
გამოიტანეს საბოლოო დასკვნა
| პარამეტრი | მოქმედება | წესი |
| A (ამპლიტუდა) | ვერტიკალური გაჭიმვა/შეკუმშვა | როცა ამპლიტუდის აბსოლუტური მნიშვნელობა |A| > 1 -ზე ფუნქციის გრაფიკი გაჭიმულია ვერტიკალურად, ხოლო 0 < |A| < 1 გრაფიკი შეკუმშულია ვერტიკალურად. |
| B (პერიოდი) | ჰორიზონტალური შეკუმშვა/გაჭიმვა | T = |
| C (ფაზური წანაცვლება) | ჰორიზონტალური გადაადგილება | C ერთეულით გადაადგილება, ნიშნის საპირისპიროდ. |
| D (ვერტიკალური წანაცვლება) | ვერტიკალური გადაადგილება | D ერთეულით გადაადგილება, ნიშნის შესაბამისად (y=D არის საშუალო ხაზი). |
ჩვენი გაშლილი გაკვეთილის პირველი ნაწილი, დეტალურად მიეძღვნა სინუსოიდური ფუნქციის A, D, B და C პარამეტრების სიღრმისეულ ანალიზს. მოსწავლეთა შედეგებმა ნათლად აჩვენა: დროის ინვესტიცია ცნებების გააზრებაში გადამწყვეტია. მოსწავლეებმა გაიაზრეს, რომ ამპლიტუდა არის მოძრაობის „ძალა“, ვერტიკალური წანაცვლება – „ცენტრი“, პერიოდი – „სიჩქარე“, ხოლო ფაზური წანაცვლება – „დროში გასწორება“.
ამ მეთოდოლოგიურმა მიდგომამ მათ ჩამოუყალიბა მყარი საფუძველი, რათა აბსტრაქტული მათემატიკური ფორმულა ექციათ ანალიზისა და ინტერპრეტაციის ინსტრუმენტად.
თუმცა, მათემატიკური წიგნიერების ჭეშმარიტი ტესტი არის ამ ცალკეული ცოდნის ინტეგრირება და კომპლექსურ, რეალურ ამოცანაში გამოყენება. მომდევნო სტატია (მეორე ნაწილი) დაეთმობა გაკვეთილის გადამწყვეტ ეტაპს, სადაც მოსწავლეებმა შექმნეს ზღვის მოქცევის ტალღის სრული მოდელი და გამოიყენეს ის პროგნოზირებისთვის. ეს ნაწილი აჩვენებს, თუ როგორ მივიღეთ სიღრმისეული გაგებიდან პრაქტიკული შედეგები.
გამოყენებული ლიტერატურა:
- ეროვნული სასწავლო გეგმა https://mes.gov.ge/content.php?id=3929&lang=geo
- მათემატიკის გზამკვლევი მე-11 კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/metertmete/
- https://courses.lumenlearning.com/suny-osalgebratrig/chapter/graphs-of-the-sine-and-cosine-functions/


