ორგანიზმების სახეობების, მათი მახასიათებლებისა და ევოლუციური კავშირების ამსახველი ბიოლოგიური მონაცემების უზარმაზარი მასივი მუდმივად მოითხოვს სისტემატიზაციას, ანალიზსა და ვიზუალიზაციას. ამ პროცესში, მათემატიკური აზროვნება მნიშვნელოვან დამხმარედ გვევლინება.
წარმოგიდგენთ შემოქმედებით დავალებას, რომელიც მე-7 კლასის მოსწავლეებს საშუალებას აძლევს, თეორიული ცოდნა – სიმრავლეების ცნებები (თანაკვეთა, გაერთიანება, ქვესიმრავლე) – უშუალოდ გამოიყენონ ცოცხალი სამყაროს კლასიფიკაციისა და შედარებისთვის.
დავალების, „ცოცხალი სამყაროს კლასიფიკაცია სიმრავლეებით“, მთავარი მიზანია, მოსწავლეებმა შექმნან მათემატიკური მოდელი – კერძოდ, ვენის დიაგრამა – რათა ვიზუალურად დაინახონ, რა არის საერთო და რა განმასხვავებელი ორ ბიოლოგიურ ჯგუფს შორის, და ამგვარად განავითარონ ლოგიკური მსჯელობის უნარი.
თემა: სიმრავლე და რიცხვითი სიმრავლეები
სამიზნე ცნებები/ ქვეცნებები
მათემატიკური მოდელი
სიმრავლე, ქვესიმრავლე; თანაკვეთა; გაერთიანება;
კანონზომიერება
სიმრავლეებს შორის მიმართებები
ლოგიკა:
სიმრავლე. ლოგიკური კავშირები და მსჯელობა.
საკითხები:
- სიმრავლის ელემენტები
- ვენის დიაგრამა
- მოქმედებები სიმრავლეებზე (თანაკვეთა, გაერთიანება), ქვესიმრავე უნივერსალური სიმრავლე, ცარიელი სიმრავლე
- ვენის დიაგრამის მეშვეობით მოქმედებების წარმოდგენა
- ვენის დიაგრამის მეშვეობით ამოცანების ახმოხსნა.
- რეალური სიტუაციის მოდელირება ვენის დიაგრამის მეშვეობით
შეფასების ინდიკატორები – მოსწავლემ უნდა შეძლოს:
- სიმრავლური ცნებებისა და ოპერაციების გამოყენება ამოცანის ამოხსნისას (მათ.საბ.7,8,9).
თემატური არეალი: სიმრავლეების თეორიის გამოყენება ბიოლოგიურ მონაცემთა კლასიფიკაციისა და ვიზუალიზაციისთვის.
ძირითადი იდეა: საერთო და განმასხვავებელი ნიშან-თვისებების ვიზუალური წარმოდგენა ვენის დიაგრამების გამოყენებით.
საკვანძო შეკითხვა: როგორ შეიძლება მათემატიკური სიმრავლეების ცნებების გამოყენება ცოცხალი ორგანიზმების მახასიათებლების გასაანალიზებლად და დასახარისხებლად?
შემოქმედებითი დავალება მოსწავლეებისათვის:
| ცოცხალი სამყაროს მრავალფეროვნება იმდენად დიდია, რომ მეცნიერებმა მისი შესწავლისთვის დაყოფა დაიწყეს სხვადასხვა ჯგუფებად — მცენარეებად, ცხოველებად, სოკოებად, ბაქტერიებად და ა.შ. ხშირად ამ ჯგუფებს საერთო ნიშნებიც აქვთ და განსხვავებულიც. მაგალითად, ცხოველებსა და მცენარეებს ორივეს სჭირდებათ სუნთქვა და საკვები, მაგრამ მცენარეები თვითონ ამზადებენ საკვებს, ხოლო ცხოველები — არა. ამ დავალების მიზანია გაიაზროთ, როგორ შეიძლება ცოცხალი სამყაროს კლასიფიკაციის ნიშნების შედარება სიმრავლეების მოქმედებების (თანაკვეთა, გაერთიანება) დახმარებით. ნაბიჯი 1: სიმრავლეების განსაზღვრა და მახასიათებლების ჩამოთვლა აირჩიეთ ორი ძირითადი სიმრავლე, რომელთა თვისებები შეიძლება შევადაროთ:
შეადგინეთ მახასიათებლების სია (სიმრავლეების ელემენტები), რომელიც ეხება ამ ორ ჯგუფს:
ნაბიჯი 2: მათემატიკური მოქმედებები სიმრავლეებზე გამოიყენეთ სიმრავლეების ცოდნა და ჩამოწერონ შედეგები:
ნაბიჯი 3: პროდუქტი – ვენის დიაგრამა შექმენით საბოლოო ვიზუალური პროდუქტი (პლაკატი/პრეზენტაცია):
|
შეფასების რუბრიკა (ფოკუსირება სიმრავლეებზე)
ეს რუბრიკა ორიენტირებულია იმაზე, თუ რამდენად სწორად გამოიყენეს მოსწავლეებმა მათემატიკური ცნებები ბიოლოგიური მონაცემების ანალიზისთვის.
| შეფასების კრიტერიუმი | დაბალი დონე
(1 ქულა) |
საშუალო დონე
(2 ქულა) |
მაღალი დონე
(3 ქულა) |
დაკავშირებული სამიზნე ცნებები |
| თემის შერჩევა, სიმრავლეების დასახელება და მახასიათებლების ჩამოწერა | სიმრავლეები მითითებულია ზედაპირულად ან არასრულია; ელემენტები არ აკავშირებენ კონკრეტულ ცოცხალ ორგანიზმებს | არჩეულია შესაბამისი მაგალითები, მაგრამ ნაწილობრივ; ნაწილობრივ ჩამოთვლილია ელემენტები, ზოგი არ შეესაბამება თემას | სწორადაა შერჩეული ცოცხალი ორგანიზმების ორი ჯგუფი (მაგ. მცენარეები და ცხოველები) და მათ შესაბამისი სიმრავლეების სახელი (A და B); ჩამოთვლილია მინიმუმ 5–6 ელემენტი თითოეული სიმრავლისთვის; ელემენტები შესაბამისია თემის და არ არის შემთხვევითი, | მათემატიკური მოდელი. სიმრავლე, სიმრავლის ელემენტი. |
| სიმრავლეებზე მოქმედებები
|
ნაწილობრივ ან არასწორადაა ნაჩვენები თანაკვეთა და გაერთიანება; ქვესიმრავლეები არ არის მითითებული | სწორადაა ნაჩვენები მინიმუმ ორი მოქმედება (A∩B, A∪B); ზოგი განსხვავება ან ქვესიმრავლე ნაწილობრივ არის | სრულად ნაჩვენებია: თანაკვეთა (A∩B), გაერთიანება (A∪B), განსხვავებები; მოსწავლემ მოიფიქრა და სწორად ჩამოაყალიბა მინიმუმ 2 ქვესიმრავლე თითოეული ძირითადი სიმრავლიდან; ჩაწერილია ზუსტად და ლოგიკურად, სიმბოლოების გამოყენებით | კანონზომიერება.
(სიმრავლეებს შორის მიმართებები. სიმრავლე, ქვესიმრავლე, თანაკვეთა, გაერთიანება,) |
| ვიზუალური წარმოდგენა (ვენის დიაგრამა) | დიაგრამა არასწორადაა შესრულებული ან მოუმწიფებელია; ელემენტები არასწორ უბნებშია | სწორადაა შესრულებული, ელემენტები ძირითადად სწორ უბნებშია, თუმცა არის ხრვეზები, ნაწილობრივ არასწორია; | სუფთად და გამოკვეთილადაა შესრულებული; ელემენტები სწორ უბნებშია; თანაკვეთის არე გამოყოფილია | მათემატიკური მოდელი. კანონზომიერება, ლოგიკა |
| ლოგიკური მსჯელობა და დასკვნა | მსჯელობა გაურკვეველია ან მხოლოდ აღწერითია; არ ჩანს ურთიერთკავშირი ელემენტებს შორის | მსჯელობა ნაწილობრივ ლოგიკურია; ნაწილობრივ ჩანს კანონზომიერებების ან განსხვავებების გაანალიზება | მსჯელობისას იყენებს ლოგიკურ კავშირებს სიმრავლეებს შორის მიმართებებზე; მსჯელობს არგუმენტირებულად; დასკვნები გამოაქვს ზუსტად | ლოგიკა. ლოგიკური კავშირები და მსჯელობა |
| შემოქმედებითობა და დამოუკიდებლობა | სამუშაო შესრულებულია მინიმალური ჩართულობით; მოსწავლე ასრულებს მხოლოდ დავალებას | ჩანს მოსწავლის მცდელობა და დამოუკიდებლობა; გარკვეული ახალი იდეები წარმოდგენილია | ნამუშევარი გამოირჩევა ორიგინალური მიდგომით, დამოუკიდებელი აზროვნებით, დამატებითი ნიმუშებით ან ვიზუალიზაციით | მათემატიკური მოდელი, ლოგიკური მსჯელობა. |
წარმოგიდგენთ რამდენიმე მოსწავლის ნამუშევარს ფოტოს სახით:
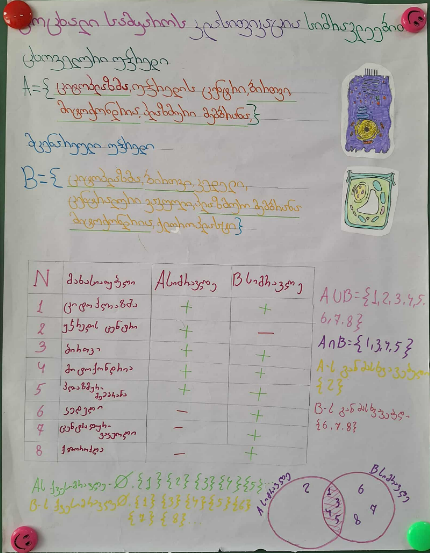 |
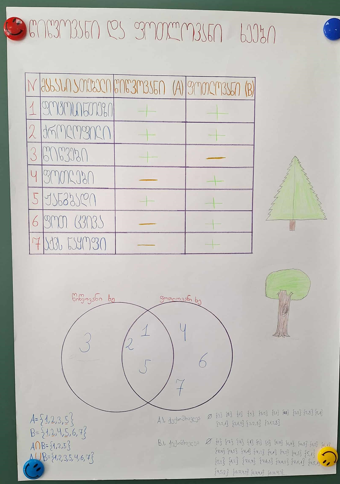 |
 |
 |
ვენის დიაგრამებზე მუშაობით, მოსწავლეებმა არა მხოლოდ შექმნეს მათემატიკური მოდელები რეალური ბიოლოგიური სიტუაციებისთვის, არამედ განავითარეს ლოგიკური მსჯელობის უნარი, რასაც თან ახლდა აღმოჩენისა და შემოქმედებითი სიამოვნება. მათ მიერ შესრულებულმა დავალებამ აჩვენა სიმრავლეების ცნებების მართვის, ცოცხალ ორგანიზმებს შორის კანონზომიერებების დანახვისა და მახასიათებლების დამოუკიდებლად კლასიფიკაციის უნარი ვიზუალური მოდელების გამოყენებით. მთელი პროცესი თითოეული მოსწავლისთვის იყო სასიამოვნო და წარმატების განცდის მომტანი. საბოლოოდ, დავალება ცხადყოფს, რომ მოსწავლეებმა სრული წარმატებით გამოიყენეს თეორიული ცოდნა პრაქტიკაში, გამოავლინეს შემოქმედებითი და დამოუკიდებელი აზროვნება, შექმნეს ვენის დიაგრამები და დამაჯერებლად ახსნეს ცოცხალი ორგანიზმების ჯგუფების საერთო და განსხვავებული ნიშნები.
გამოყენებული ლიტერატურა
- ეროვნული სასწავლო გეგმა https://mes.gov.ge/content.php?id=3929&lang=geo
- მათემატიკის გზამკვლევი მეშვიდე კლასი. შედგენილი ქეთი ცერცვაძის მიერ, ზოგადი განათლების რეფორმის ფარგლებში. https://math.ge/meshvide-klasi/
- ლიტერატურა: მე-7 კლასი. მათემატიკა. (დანართი11. სიმრავლეები) ავტორი ქეთი ცერცვაძე https://drive.google.com/drive/folders/1BeBNZuzEyGqAcGqbP8j9sr-iiWwEgzYL


