„გლახა სიტყვა მათრახიაო“, „ბევრი სიტყვა მახვილზე მეტად მჭრელიაო“ – კიდევ ბევრი ანდაზის თუ იდიომის მოძებნა შეიძლება იმის დასასაბუთებლად, რომ სიტყვას დიდი ძალა აქვს. მარტო სახარება რად ღირს? – „ყველა სიტყვას აქვს ძალა და ძალაუფლება“ (მათე 12:36,37).
დავუბრუნდეთ ჩვენს ფიზიკას. აქაც ასეა თურმე. ფიზიკაშიც დიდი ძალა აქვს თუნდაც ერთ სიტყვას. მაგალითად, წინადადებაში ერთი სიტყვის ყოფნა-არყოფნა განსაზღვრავს, რა ტიპის მოძრაობასთან გვაქვს საქმე.
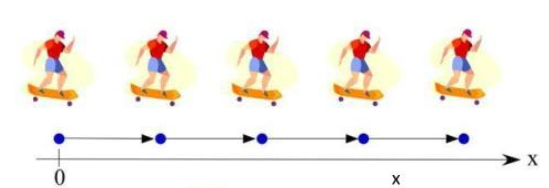
განვიხილოთ სკეიტბორდის ისეთი მოძრაობა, რომლის დროსაც იგი ყოველ 10წმ-ში ტოლ მანძილებს გადის (ნახ.1).
ნახ. 1
როგორც ვხედავთ, სკეიტბორდის მოძრაობის ტრაექტორია წრფეა, შესაბამისად, მოძრაობა წრფივია.
ვთქვათ საწყის t0 მომენტში სკეიტბორდი კოორდინატთა სათავეშია (0 წერტილი). მის მიერ განვლილი მანძილი დროის განმავლობაში იზრდება შემდეგი კანონზომიერებით: სკეიტბორდი ყოველ 10წმ-ში გადის 20მ-ს.
შეიძლება თუ არა წარმოდგენილი მოძრაობა ჩავთვალოთ წრფივ თანაბარ მოძრაობად?
იმისთვის, რომ მოძრაობა იყოს წრფივი თანაბარი, საჭიროა სხეული დროის ნებისმიერ ტოლ შუალედში ტოლ მანძილებს გადიოდეს. როგორც ვხედავთ, განმარტებაში გაჩნდა სიტყვა „ნებისმიერი“. სწორედ ამ სიტყვის მნიშვნელობაზე ვსაუბრობდით დასაწყისში. რას ნიშნავს ეს სიტყვა?
სიტყვა „ნებისმიერი“ ნიშნავს იმას, რომ მოძრაობის დრო რაც არ უნდა მცირე ინტერვალებად დავყოთ, შესაბამისი განვლილი მანძილები უნდა იყოს ერთნაირი. როგორც წარმოდგენილი ამოცანის პირობებით არის განსაზღვრული, სკეიტბორდი ყოველი 10წმ-ის განმავლობაში ერთნაირ მანძილს – 20მ-ს გადის. დავყოთ ეს დრო შედარებით უფრო მცირე ინტერვალებად. ისევ თანაბარი იქნება თუ არა სკეიტბორდის მიერ განვლილი მანძილები ყოველ 5 წმ-ში? ან ყოველ 1 წმ-ში? ამოცანის პირობები ამის შესახებ არაფერს ამბობს. შესაბამისად, ვერაფერს ვიტყვით იმაზე, არის თუ არა სკეიტბორდის მიერ შესრულებული მოძრაობა წრფივი თანაბარი.
ამრიგად, თუ მოძრაობის პირობების აღწერისას დაზუსტებული არ არის, რომ სხეული დროის ნებისმიერ ტოლ შუალედში ტოლ მანძილს გადის, წრფივ თანაბარ მოძრაობაზე დაზუსტებით საუბარი არასწორი იქნება.
წრფივი თანაბარი მოძრაობის სიჩქარე
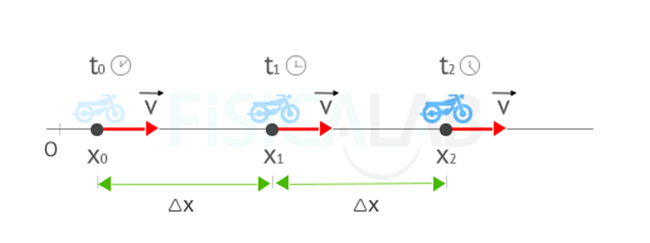
ნახ. 2
განვიხილოთ მოტოციკლის წრფივი თანაბარი მოძრაობის მაგალითი (ნახ.2). ვთქვათ, საწყის t0 მომენტში მოტოციკლი კოორდინატთა სათავიდან (0 წერტილი) X0 მანძილით იყო დაშორებული. ეს კი ნიშნავს, რომ მისი საწყისი კოორდინატი იყო X0. t1 = 10 წთ დროის გასვლის შემდეგ მოტოციკლი აღმოჩნდა X1 წერტილში. ე. ი. მისი კოორდინატი გახდა X1. ხოლო Δ X = X1 – X0.
აქ ΔX რეალურად მოტოციკლის მიერ განვლილ მანძილს და გადაადგილების მოდულს ემთხვევა. ამ შემთხვევაში განვლილი მანძილი და გადაადგილების მოდული ერთმანეთის ტოლია, რადგან სხეული არ იცვლის მიმართულებას, ამასთან მოძრაობს წრფივად. შემდეგი t2 = 10 წთ-ის გავლის შემდეგ მოტოციკლის კოორდინატი გახდა X2. როგორც ნახაზიდან ჩანს, დროის ამ ინტერვალშიც განვლილი მანძილი (გადაადგილების მოდული) ემთხვევა წინა 10 წთ-ში განვლილი მანძილს (გადაადგილების მოდულს) ΔX = X2 – X1.
გავიხსენოთ, რომ
ლიტერატურა
- გიორგი გედენიძე, ეთერ ლაზარაშვილი, ფიზიკა VII კლასი. 2001 წ;
- ელენე სურგულაძე. მანანა კასრაძე. ფიზიკა VII კლასი. 2003 წ;
- ილუსტრაციები აღებულია ვებგვერდებიდან:
https://www.slideserve.com/emilie/motion-with-constant-velocity-in-1d