მექანიკა ვრცელი თემაა და კიდევ ბევრს დავწერთ ამ მიმართულებითო – ავღნიშნეთ წინა სტატიაში. ამდენად ვაგრძელებთ მექანიკის შესასწავლად საჭირო ცნებების და შესაბამისი მათემატიკურ აპარატის გაცნობას. ჩვენ უკვე შევისწავლეთ ფიზიკურ სიდიდე – განვლილი მანძილი, რომელსაც სხვანაირად გავლილ გზასაც უწოდებენ. მექანიკაში ხშირად ხდება საჭირო ისეთი ამოცანების გადაწყვეტა, სადაც საჭიროა დამატებით ვიცოდეთ იმ მონაკვეთის მიმართულება, რომელიც ნივთიერი წერტილის საწყის მდებარეობას მის საბოლოო მდებარეობასთან აერთებს.
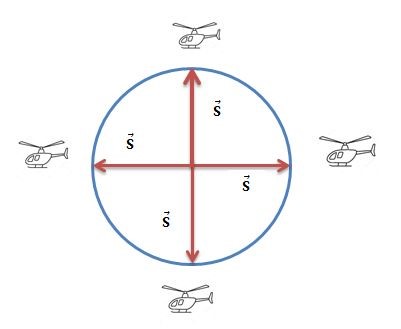
განვიხილოთ მაგალით: იპოვეთ ვერტმფრენის მდებარეობა, რომელიც აეროპორტიდან აფრინდა და რაღაც დროში გაიარა 150კმ. მიუხედავად იმისა, რომ ვიცით მის მიერ გავლილი მანძილი, წარმოუდგენელია ვერტმფრენის ადგილსამყოფელის აღმოჩენა, თუ არ გვეცოდინება რა მიმართულებით გაფრინდა, რადგან კონკრეტულ დროს იგი S რადიუსიანი წრეწირის ნებისმიერ წერტილში შეიძლება იმყოფებოდეს.
ნახ. 1
ანუ ვერტმფრენის მდებარეობის დასადგენად დამატებით გვესაჭიროება მისი მოძრაობის მიმართულების ცოდნა.
წრფის მიმართულ მონაკვეთს, რომელიც სხეულის საწყის მდებარეობას მის საბოლოო მდებარეობასთან აერთებს, გადაადგილება ეწოდება . ეს სიდიდე ხასიათდება როგორც რიცხვითი მნიშვნელობით, ასევე მიმართულებით. ისევე, როგორც განვლილი მანძილის, მისი საზომი ერთეულებიც არის მ, სმ, დმ, კმ და ა. შ. SI სისტემაში კი მას მეტრებში ზომავენ. გადაადგილებას სქემატურად ისრიანი მონაკვეთით გამოსახავენ. ამდენად, თუ გვეცოდინება საიდან აფრინდა ვერტმფრენი (საწყისი მდებარეობა) და რა გადაადგილება შეასრულა, მისი საბოლოო მდებარეობის პოვნა შესაძლებელი იქნება.
ასე, რომ უკვე შემოვიტანეთ ფიზიკური სიდიდე, გადაადგილება, რომელიც რიცხვით მნიშვნელობასთან ერთად მიმართულებითაც ხასიათდება. ისეთ სიდიდეებს, რომლებიც რიცხვითი მნიშვნელობის გარდა მიმართულებითაც ხასიათდება, ვექტორულ სიდიდეებს უწოდებენ ასეთი სიდიდეები ფიზიკიაში ბევრია: გადაადგილება, სიჩქარე, ძალა და ა.შ.
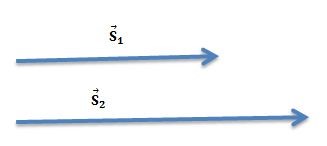
ნახ.2-ზე გამოსახულია ორი გადაადგილების ვექტორი . ისრიანი მონაკვეთის სიგრძე გარკვეული მასშტაბით გვიჩვენებს ვექტორული სიდიდის რიცხვით მნიშვნელობას, ხოლო ისარი, ამ სიდიდის მიმართულებას. ვექტორული სიდიდის რიცხვით მნიშვნელობას ვექტორის მოდულსაც უწოდებენ. ვექტორის მოდულს აღნიშნავენ იმავე ასოთი ისრის გარეშე. მაგალითად, გადაადგილების – ის მოდულია S.
ნახ. 2
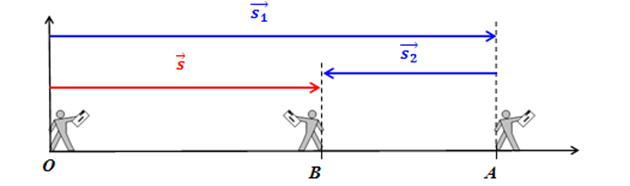
ვექტორული სიდიდის, გადაადგილების უკეთ გასაცნობად განვიხილოთ მაგალითი (ნახ.3). მოსწავლე O წერტილიდან დაიძრა და მივიდა ჯერ A წერტილში 10მ, შემდეგ კი B წერტილში 4მ. ვიპოვოთ მოსწავლის გადაადგილება და განვლილი მანძილი. განმარტების თანახმად, მოსწავლის გადაადგილების იქნება მონაკვეთის სიგრძის ტოლი = 10 – 4 = 6მ, ხოლო განვლილი მანძილი S = 10 + 4 = 14მ.
ნახ. 3
ანუ განვლილი მანძილი არის იმ გზის სიგრძე, რაც მოსწავლემ უშუალოდ გაიარა, ხოლო გადაადგილება – მოსწავლის საწყისი და საბოლოო მდებარეობის შემაერთებელი წრფის მიმართული მონაკვეთი. როგორც უკვე მივხვდით, განვლილი მანძილი ვექტორს არ წარმოადგენს. ის სკალარული სიდიდეა და ხასიათდება მხოლოდ რიცხვითი მნიშვნელობით. ამდენად, სკალარულ სიდიდეებს უწოდებენ ისეთ სიდიდეებს, რომლებიც მხოლოდ რიცხვითი მნიშვნელობით ხასიათდება. სკალარული სიდიდეა დრო, ტემპერატურა, მასა და ა.შ. სკალარული სიდიდეების შეკრება მარტივად, ალგებრულად ხდება. ამიტომაც შევკრიბეთ 10მ და 4მ განვლილი მანძილის გამოსათვლელად. ვექტორული სიდიდეების შეკრება კი გეომეტრიულად ხდება. გეომეტრიულ შეკრება-გამოკლებას მომავალში გავეცნობით.
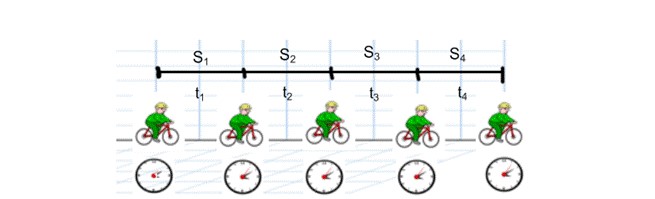
მექანიკაში სხვადასხვა სახის მოძრაობა განიხილება. მათ შორის უმარტივეს სახეს წარმოადგენს წრფივი თანაბარი მოძრაობა. როგორც სახელიდან უკვე მივხვდით, ამ მოძრაობის ტრაექტორია არის წრფე, ხოლო თანაბარი ეწოდება იმიტომ რომ სხეული თანაბარ დროში თანაბარ მანძილებს გადის. უფრო ზუსტად კი წრფივი თანაბარი მოძრაობა ეწოდება ისეთ მოძრაობას, რომლის დროსაც სხეული დროის ნებისმიერ ტოლ შუალედში ტოლ მანძილს გადის (ნახ.3).
ნახ. 4
ვთქვათ ველოსიპედისტი ყოველ წუთში გადის 40მ, არის თუ არა ეს მოძრაობა თანაბარი? ერთი შეხედვით მოძრაობა თანაბარია, რადგან პირობის მიხედვით, სხეული დროის თანაბარ შუალედში – ყოველ ერთ წუთში თანაბარ მანძილს, 40მ-ს გადის, მაგრამ ამოცანა არაფერს გვეუბნება ყოველ ნახევარ წუთში გადის თუ არა სხეული 20მ-ს, ან ყოველ მეოთხედ წუთში – 10მ-ს. ამიტომ შეიძლება ისეც მოხდეს, რომ სხეულმა ყოველ ერთ წუთში გაიაროს 40მ ისე, რომ პირველ ნახევარ წუთში გაიაროს 10მ და შემდეგ ნახევარ წუთში – 30მ, ანუ ყოველ ნახევარ წუთში – განსხვავებული მანძილები. ეს კი აღარ იქნება თანაბარი მოძრაობა. სწორედ ამიტომ თანაბარი მოძრაობის განმარტებაში ხაზი აქვს გასმული სიტყვას „ნებისმიერ“,რაც ნიშნავს იმას, რომ დროის შუალედის ნებისმიერი შემცირებისას, გადაადგილებაც შესაბამისად უნდა შემცირდეს. ამგვარად, მოცემულ ამოცანას ასე უნდა ვუპასუხოთ – ამოცანის პირობებიდან გაურკვეველია, არის თუ არა მოცემული მოძრაობა თანაბარი.
ჩვეუ უკვე რამდენჯერმე ვახსენეთ ფრაზა „სხეულის მოძრაობის შესწავლა“. რას ნიშნავს ეს? სხეულის მოძრაობის შესწავლა ნიშნავს სხეული მდებარეობის პოვნას სივრცეში დროის კონკრეტულ მომენტში სხვა სხეულის მიმართ. გარკვეულ მომენტში სხეულის მდებარეობის ცოდნას ხშირად პრაქტიკული მნიშვნელობა აქვს. მაგალითად, ერთსა და იმავე გზას დროის ერთი და იმავე შუალედში ადამიანი და ავტომობილი სხვადასხვა დროს ანდომებს და შესაბამისად, ვხვდებით, რომ მათი ერთი წერტილიდან ერთდროულად გასვლისას, დანიშნულების ადგილზე ეს ორი სხეული სხვადასხვა დროს აღმოჩნდება.
რისი ცოდნაა საჭირო იმისთვის, რომ დავადგინოთ რა მანძილს გაივლის სხეული თანაბარი მოძრაობისას დროის მოცემულ შუალედში? ვთქვათ, ვიცით, რომ იგი დროის ერთეულში, ერთ წამში გადის 5მ-ს, მაშინ 2წმ-ში გაივლის 10მ-ს, 3წმ-ში – 15მ-ს და ა. შ. ესე იგი მოცემულ დროის ინტერვალში განვლილი მანძილი რომ ვიპოვოთ, საჭიროა ერთ წმ-ში განვლილი მანძილი გავამრავლოთ დროის ინტერვალზე. დროის ერთეულში (ერთ წმ-ში) განვლილი მაძილი საზოგადოდ, მოძრაობის სისწრაფეს ახასიათებს და მას სიჩქარეს უწოდებენ. ანუ, თუ გვეცოდინება სხეულის სიჩქარე, მას გავამრავლებთ დროზე და მივიღებთ თანაბრად მოძრავი სხეულის მიერ ამ დროში განვლილ მანძილს.
ჩვენ უკვე ავღნიშნეთ, რომ მოძრაობა და უძრაობა ფარდობითია. შესაბამისად, ფარდობითი იქნება სხეულის სიჩქარე, რადგან იგი განვლილ მაძილთან არის დაკავშირებული, და როგორც უკვე ვიცით სხეული მოძრაობისას სხვადასხვა სხეულის მიმართ სხვადასხვა მანძილს გადის. ესე იგი ავტომობილის სიჩქარე ხის მიმართ თუ გარკვეული სიდიდია, იგივე მოძრაობისას ავტომობილის სიჩქარე სარკის მიმართ ნულია.
ამგვარად ამ სტატიაში გავეცანით მექანიკური მოძრაობის უმარტივეს სახეს – თანაბარ მოძრაობას და მასთან დაკავშირებულ ფიზიკურ სიდიდეებს.
ლიტერატურა
- გიორგი გედენიძე, ეთერ ლაზარაშვილი, ფიზიკა VII კლასი. 2001 წ;
2 ელენე სურგულაძე. მანანა კასრაძე. ფიზიკა VII კლასი. 2003 წ;
- ილუსტრაციები აღებულია ვებ-გვერდიდან